【题目】阅读材料,善于思考的小军在解方程组 ![]() 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5
即2(2x+5y)+y=5③
把方程①代入③得:2×3+y=5
∴y=﹣1
把y=﹣1代入①得x=4
∴方程组的解为 ![]()
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组 ![]()
(2)已知x、y满足方程组 ![]()
①求x2+4y2的值;
②求 ![]() 的值.
的值.
参考答案:
【答案】
(1)解:由②得:3x+6x﹣4y=19,即3x+2(3x﹣2y)=19③,
把①代入③得:3x+10=19,即x=3,
把x=3代入①得:y=2,
则方程组的解为 ![]() ;
;
(2)解:①由5x2﹣2xy+20y2=82得:5(x2+4y2)﹣2xy=82,即x2+4y2= ![]() ,
,
由2x2﹣xy+8y2=32得:2(x2+4y2)﹣xy=32,即2× ![]() ﹣xy=32,
﹣xy=32,
整理得:xy=4,
∴x2+4y2= ![]() =
= ![]() =18;
=18;
②∵x2+4y2=18,xy=4,
∴(x+2y)2=x2+4y2+4xy=18+16=34,即x+2y=± ![]() ,
,
则原式= ![]() .
.
【解析】(1)“整体代换”可以一个未知数系数为基准,在此基础上乘以一个适当的数,另一个未知数系数进行拆分;(2)以(x2+4y2)为个整体,两个方程分别变形,整体上以(x2+4y2)、xy为两个未知数,加减消元,消去xy ,即可求出(x2+4y2)的值;x2+4y2相当于x、2y的平方和,联想到这两个数的平方,分别代换即可求出x+2y的值,注意正负都可取.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具经销店在开学时购进了A、B两种型号的计算器,已知:购进A型号的计算器20个,B型号的计算器25个需用1265元;购进A型号的计算器16个,B型号的计算器12个需用748元.求:
(1)A、B两种型号的计算器进价分别是多少元?
(2)在(1)的条件下,若A型号的计算器的售价是30元/个,B型号的计算器的售价是45元/个,商店一次性购进两种型号的计算器各20个,并全部销售,求商店所获利润是多少元?
(3)在两种型号计算器的进价和售价均保持不变的情况下,该商店准备购进A、B两种型号的计算器共40个,且A型号的计算器的数量不得少于5个,问:商店应怎样进货,才能使所获利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距300千米,甲、乙两辆汽车同时分别从A、B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(千米)都是行驶时间t(时)的一次函数,图象如图所示,请利用所结合图象回答下列问题:
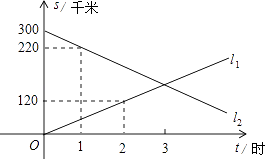
(1)甲的速度为 , 乙的速度为;
(2)求出:l1和l2的关系式;
(3)问经过多长时间两车相遇. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.
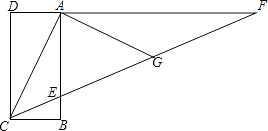
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2﹣2y=1,那么4x2﹣8y+5= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量
1本
2本
3本
3本以上
人数(人)
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数
B.中位数
C.众数
D.方差 -
科目: 来源: 题型:
查看答案和解析>>【题目】说明代数式[(x﹣y)2﹣(x+y)(x﹣y)]÷(﹣2y)+y的值,与y的值无关.
相关试题

