【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.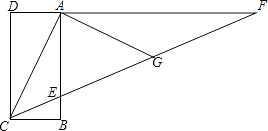
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高?
参考答案:
【答案】
(1)解:∵四边形ABCD是长方形,
∴DF∥BC,
∴∠AFC=∠ECB,
∵AC=AG,
∴∠ACG=∠AGC,
∵∠ACG=2∠GAF,∠AGC=∠GAF+∠F,
∴∠F=∠FAG,
∴∠ACG=2∠ECB,
∴∠ACB=∠ACG+∠ECB=3∠ECB=60°,
∴∠ECB=20°;
(2)解:设△AEF中EF边上的高为hcm,
∵∠F=∠FAG,
∴AG=GF,
∵∠BAF=90°,
∴∠EAG+∠GAF=90°,∠AEF+∠EFA=90°,
∴∠EAG=∠AEG,
∴EG=AG=GF,
∴EF=2AG=2×6.5=13(cm),
∴AE= ![]() =5(cm),
=5(cm),
∵△AEF的面积= ![]() AEAF=
AEAF= ![]() EFh,
EFh,
解得:h= ![]() cm,
cm,
即△AEF中EF边上的高为 ![]() cm.
cm.
【解析】(1)可利用平行线的性质,内错角相等可转化∠ECB=∠AFC,再由“AG=AC,∠ACG=2∠GAF”得出∠F=∠FAG,进而得出∠ACB=∠ACG+∠ECB=3∠ECB=60°,最后求出∠ECB的度数;(2)可证出EG=AG=GF,由勾股定理求出AE,再由面积法,即△AEF的面积= ![]() AEAF=
AEAF= ![]() EFh,求出h.
EFh,求出h.
【考点精析】掌握三角形的面积和等腰三角形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
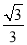 x﹣
x﹣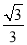 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .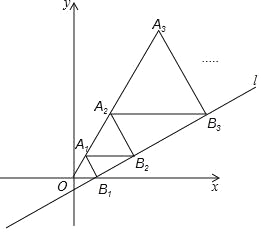
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具经销店在开学时购进了A、B两种型号的计算器,已知:购进A型号的计算器20个,B型号的计算器25个需用1265元;购进A型号的计算器16个,B型号的计算器12个需用748元.求:
(1)A、B两种型号的计算器进价分别是多少元?
(2)在(1)的条件下,若A型号的计算器的售价是30元/个,B型号的计算器的售价是45元/个,商店一次性购进两种型号的计算器各20个,并全部销售,求商店所获利润是多少元?
(3)在两种型号计算器的进价和售价均保持不变的情况下,该商店准备购进A、B两种型号的计算器共40个,且A型号的计算器的数量不得少于5个,问:商店应怎样进货,才能使所获利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距300千米,甲、乙两辆汽车同时分别从A、B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(千米)都是行驶时间t(时)的一次函数,图象如图所示,请利用所结合图象回答下列问题:
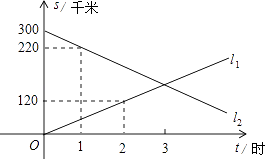
(1)甲的速度为 , 乙的速度为;
(2)求出:l1和l2的关系式;
(3)问经过多长时间两车相遇. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,善于思考的小军在解方程组
 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5
即2(2x+5y)+y=5③
把方程①代入③得:2×3+y=5
∴y=﹣1
把y=﹣1代入①得x=4
∴方程组的解为
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组
(2)已知x、y满足方程组
①求x2+4y2的值;
②求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2﹣2y=1,那么4x2﹣8y+5= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量
1本
2本
3本
3本以上
人数(人)
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数
B.中位数
C.众数
D.方差
相关试题

