【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?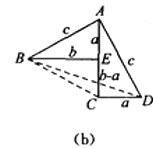
参考答案:
【答案】解:方法1:∵由图(a)可知S正方形ACFD=S四边形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的边长为b, SRt△BAE= ![]() ,SRt△BFE=
,SRt△BFE= ![]()
∴b2 = ![]() +
+ ![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2+b2=c2
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),
则AE=a,BE=b,AB=c,EC=b-a
由图(b),S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵SRt△BAE = ![]() , SRt△ACD =
, SRt△ACD = ![]() ,SRt△BEC=
,SRt△BEC= ![]() ,
,
SRt△BAD= ![]() ,S△BCD=
,S△BCD= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]()
即2ab+b(b-a)= c2 +a(b-a)
整理得: a2+b2=c2
【解析】方法1:由图(a)可知S正方形ACFD=S四边形ABFE ,S正方形ACFD=S△BAE+S△BFE,根据已知即可证得a2+b2=c2;
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),分别表示出AE、BE、CE的长,,S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD,建立方程即可证得a2+b2=c2。
【考点精析】利用三角形的面积对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】9的平方根是( )
A. 3 B. -3 C. ±3 D. ±6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的方程3x=10-ax的解,则a=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线 成轴对称的△A
成轴对称的△A  ;
;
(2)线段 被直线
被直线  ;
;
(3)在直线 上找一点P,使PB+PC的长最短,并算出这个最短长度.
上找一点P,使PB+PC的长最短,并算出这个最短长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-3b=2,则(3b-a)2+4(a-3b)-17=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)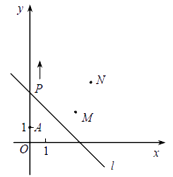
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.


(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=
 ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
相关试题

