【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线 ![]() 成轴对称的△A
成轴对称的△A ![]() ;
;
(2)线段 ![]() 被直线
被直线 ![]() ;
;
(3)在直线 ![]() 上找一点P,使PB+PC的长最短,并算出这个最短长度.
上找一点P,使PB+PC的长最短,并算出这个最短长度.
参考答案:
【答案】
(1)解:如图所示:
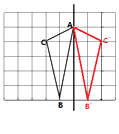
(2)垂直平分
(3)解:连接BC’交l于点P,如图,在 ![]() BC’D中
BC’D中
![]()
![]() ∴
∴ ![]() ∴最短长度为5
∴最短长度为5
【解析】(1)根据轴对称图形的性质画出对称轴。
(2)根据轴对称图形的性质可得出结论。
(3)根据作图可知点C和点C’关于直线l对称,因此连接BC’交l于点P,根据直角三角形的勾股定理可以求出线段的长度。
【考点精析】通过灵活运用轴对称的性质和作轴对称图形,掌握关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上;画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】木工师得要将一根木条固定在墙上,通常需要钉两根钉子,请你写出这一现象反映的一个数学基本事实______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】9的平方根是( )
A. 3 B. -3 C. ±3 D. ±6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的方程3x=10-ax的解,则a=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?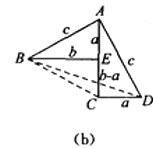
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-3b=2,则(3b-a)2+4(a-3b)-17=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)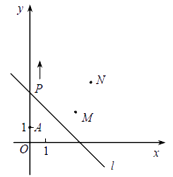
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
相关试题

