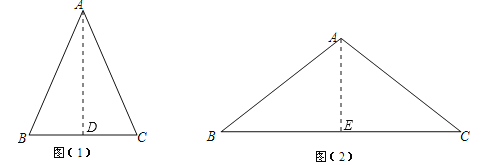
【题目】我们定义:等腰三角形中底边与腰的比叫作底角的邻对(can).如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB=![]() .容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1) . can30°=______ __;
(2) . 如图②,已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.

参考答案:
【答案】(1)![]() ;(2)18
;(2)18![]()
【解析】试题分析:(1)过点A作AD⊥BC于点D,根据∠B=30°,可得出BD=![]() AB,结合等腰三角形的性质可得出BC=
AB,结合等腰三角形的性质可得出BC=![]() AB,继而得出canB;
AB,继而得出canB;
(2)过点A作AE⊥BC于点E,根据canB=![]() ,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
试题解析:解:(1)过点A作AD⊥BC于点D,∵∠B=30°,∴cos∠B=![]() =
=![]() ,∴BD=
,∴BD=![]() AB,∵△ABC是等腰三角形,∴BC=2BD=
AB,∵△ABC是等腰三角形,∴BC=2BD=![]() AB,故can30°=
AB,故can30°=![]() =
=![]() ;
;
(2)过点A作AE⊥BC于点E,∵canB=![]() ,则可设BC=8x,AB=5x,∴AE=
,则可设BC=8x,AB=5x,∴AE=![]() =3x,∵S△ABC=24,∴
=3x,∵S△ABC=24,∴![]() BC×AE=12x2=24,解得:x=
BC×AE=12x2=24,解得:x=![]() ,故AB=AC=
,故AB=AC=![]() ,BC=
,BC=![]() ,从而可得△ABC的周长为
,从而可得△ABC的周长为![]() .
.
-
科目: 来源: 题型:
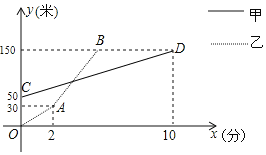
查看答案和解析>>【题目】一直线上有A、B、C不同三地,甲、乙两人分别从A、B两地同时同向出发前往距离B地150米的C地,甲、乙两人距离B地的距离y(米)与行走试卷x(分)之间的关系图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速行走,且乙在加速后的速度是甲速度的4倍.
(1)乙加速之后的速度为 米/分;
(2)求当乙追上甲时两人与B地的距离;
(3)当甲出发 分钟时,两人相距10米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
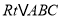 中,
中,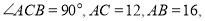 分别以
分别以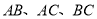 为边在
为边在 的同侧作正方形
的同侧作正方形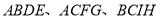 ,则图中阴影部分的面积之和为_______.
,则图中阴影部分的面积之和为_______.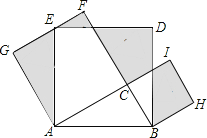
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
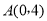 ,点
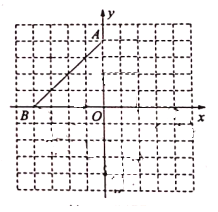
,点 .
.
(1)①画出线段
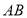 关于
关于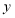 轴对称的线段
轴对称的线段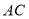 ,则点
,则点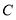 的坐标为 ;
的坐标为 ;②将线段
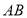 平移至
平移至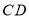 ,其中点
,其中点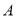 与点
与点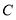 对应,画出线段
对应,画出线段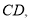 并写出点
并写出点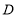 的坐标;
的坐标;(2)点
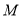 在(1)中四边形
在(1)中四边形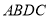 边
边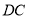 上,且
上,且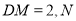 是对角线
是对角线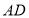 上--动点,则
上--动点,则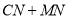 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决问题
材料一:《孟子》中记载有一尺之棰,日取其半,万世不竭,其中蕴含了“有限”与“无限”的关系.如果我们要计算到第n天时,累积取走了多长的木棒?可以用下面两种方法去解决:
方法一:第n天,留下了
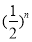 尺木棒,那么累积取走了
尺木棒,那么累积取走了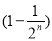 尺木棒.
尺木棒.方法二:第1天取走了
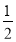 尺木棒,第2天取走了
尺木棒,第2天取走了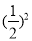 尺木棒,……第n天取走了
尺木棒,……第n天取走了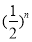 尺木棒,那么累积取走了:
尺木棒,那么累积取走了: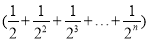 尺木棒.
尺木棒.设:
 ……①
……①由①×
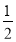 得:
得: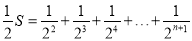 ……②
……②①-②得:
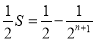 则:
则: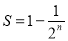
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问题:1+2+3+…+100=?据说当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确的答案:(1+100)+(2+99)+…+(50+51)=101×50=5050.
也可以这样理解:令S=1+2+3+4+…+100 ①,则S=100+99+98+…+3+2+1②
①+②得:2S=(1+100)+(2+99)+(3+98)+…+(100+1)=100×(1+100)
即
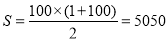
请用你学到的方法解决以下问题:
(1)计算:
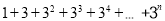 ;
;(2)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层的2倍,问塔的顶层共有多少盏灯?
(3)某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动,某一周,这款软件的激活码为下面数学问题的答案:已知一列数1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,……其中第1项是
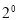 ,接下来的两项是
,接下来的两项是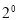 ,
,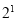 ,再接下来的三项是
,再接下来的三项是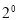 ,
,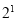 ,
,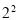 ,以此类推,求满足如下条件的正整数N:
,以此类推,求满足如下条件的正整数N: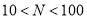 ,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

相关试题

