【题目】如图,![]() 中,
中,![]() 分别以
分别以![]() 为边在
为边在![]() 的同侧作正方形
的同侧作正方形![]() ,则图中阴影部分的面积之和为_______.
,则图中阴影部分的面积之和为_______.
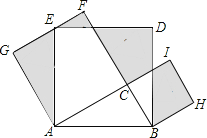
参考答案:
【答案】![]()
【解析】
过D作BF的垂线交BF于N,连接DI,通过证明S1+S2+S3+S4=Rt△ABC的面积×3,依此即可求解.
解:过D作BF的垂线交BF于N,连接DI,
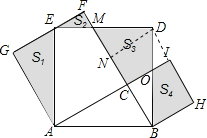
∵四边形![]() 、四边形
、四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
∴GA=AC=GF,∠G=∠ABD=90°,AE=AB=BD,BC=CI,∠H=∠ICB=90°,
∵DN⊥BF,
∴∠DNB=90°,∠NDB+∠NBD=90°,
又∵∠ABD=∠NBA+∠NBD=90°,
∴∠NBA=∠NDB,
在△ACB和△BND中
∵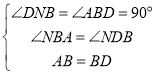
∴△ACB≌△BND(AAS),
∴BC=DN=IC,BN=AC,
又∵∠DNB=∠ICB=90°,
∴DN∥CI,
∴四边形DNCI是平行四边形,且平行四边形DNCI是矩形,
∴∠DIC=90°,
∴D、I、H三点共线,
∵∠ACB=90°,
∴∠G=∠ACB=90°,
在![]() 和
和![]() 中
中
∵![]()
∴![]() ≌
≌![]() (HL)
(HL)
∴GE=BC,
同理可证![]() ≌
≌![]() ,
,
∵∠BDE=∠ICB=90°,
∴∠DBM+∠DMB=90°,∠DBM+∠AOB=90°,
∴∠DMB=∠AOB,
∴∠EMF=∠DOI,
在△MND和△BCO中,
∵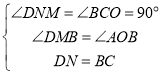
∴△MND≌△BCO,
∵DI=BN-BC,EF=GF-GE,
∴EF=DI,
在△EFM和△DIO中
∵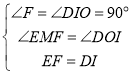
∴△EFM≌△DIO,
∵![]()
∴![]() ,
,
∴Rt△ABC的面积=![]() ,
,
∴S1+S2+S3+S4
=S1+S3+(S2+S4),
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中,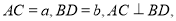 顺次连接四边形
顺次连接四边形 各边中点,得到四边形
各边中点,得到四边形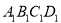 ,再顺次连接四边形
,再顺次连接四边形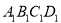 各边中点,得到四边形
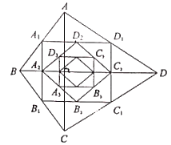
各边中点,得到四边形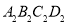 ...如此进行下去,得到四边形
...如此进行下去,得到四边形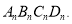 则下列结论正确的个数有( )
则下列结论正确的个数有( )①四边形
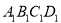 是矩形;②四边形
是矩形;②四边形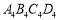 是菱形;③四边形
是菱形;③四边形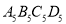 的周长为
的周长为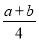 ; ④四边形
; ④四边形 的面积是
的面积是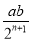 .
.
A.
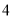 个B.
个B.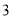 个C.
个C.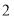 个D.
个D.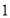 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形
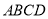 的边
的边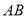 为边作等边三角形
为边作等边三角形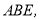 连接
连接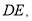 则
则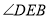 的度数为______.
的度数为______. -
科目: 来源: 题型:
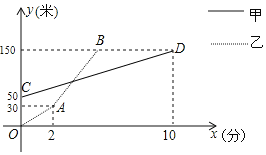
查看答案和解析>>【题目】一直线上有A、B、C不同三地,甲、乙两人分别从A、B两地同时同向出发前往距离B地150米的C地,甲、乙两人距离B地的距离y(米)与行走试卷x(分)之间的关系图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速行走,且乙在加速后的速度是甲速度的4倍.
(1)乙加速之后的速度为 米/分;
(2)求当乙追上甲时两人与B地的距离;
(3)当甲出发 分钟时,两人相距10米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
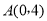 ,点
,点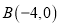 .
.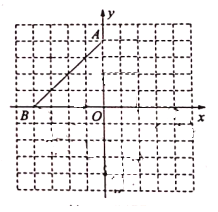
(1)①画出线段
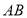 关于
关于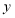 轴对称的线段
轴对称的线段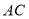 ,则点
,则点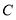 的坐标为 ;
的坐标为 ;②将线段
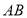 平移至
平移至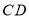 ,其中点
,其中点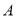 与点
与点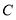 对应,画出线段
对应,画出线段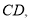 并写出点
并写出点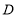 的坐标;
的坐标;(2)点
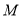 在(1)中四边形
在(1)中四边形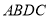 边
边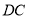 上,且
上,且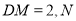 是对角线
是对角线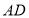 上--动点,则
上--动点,则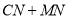 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:等腰三角形中底边与腰的比叫作底角的邻对(can).如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB=
 .容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题: (1) . can30°=______ __;
(2) . 如图②,已知在△ABC中,AB=AC,canB=
 ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.

相关试题

