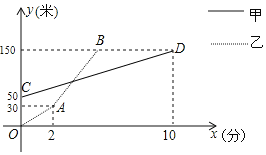
【题目】一直线上有A、B、C不同三地,甲、乙两人分别从A、B两地同时同向出发前往距离B地150米的C地,甲、乙两人距离B地的距离y(米)与行走试卷x(分)之间的关系图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速行走,且乙在加速后的速度是甲速度的4倍.
(1)乙加速之后的速度为 米/分;
(2)求当乙追上甲时两人与B地的距离;
(3)当甲出发 分钟时,两人相距10米?
参考答案:
【答案】(1)40;(2)![]() 米;(3)3或
米;(3)3或![]()
【解析】
(1)由图象可以得出开始时A、B、C有位置关系是A在B、C之间,距B地50米,乙从B地出发,前两分钟走了30米,然后提速,甲从A地出发,速度不变,10分钟到了C地,共行了100米。根据行程问题的数量关系可得出答案。
(2)用待定系数法求出直线AB、CD的解析式,并进而联立成方程组求解,可得到答案。
(3)设当甲出发t分钟时,两人相距10米,分两种情况列出方程求解可得到答案。
解:(1)如图,
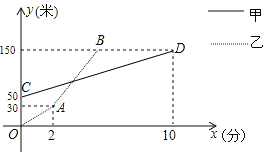
由题意甲的速度为(150-50)÷10=10米/分,
∴乙加速后的速度为40米/分,
故答案为:40
(2) 由题意A(2,30),
乙从A到B的时间![]()
∴B(5,150),
∴直线AB的解析式为y=40x-50,
∵C(0,50),D(10,150),
∴直线CD的解析式为y=10x+50,
由![]() 解得
解得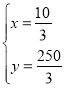
∴那么他们出发![]() 分钟时,乙追上了甲.此时两人与B地的距离为
分钟时,乙追上了甲.此时两人与B地的距离为![]() 米。
米。
(3)设当甲出发t分钟时,两人相距10米,
①若乙在甲的后面,列方程得:
15×2+40(t-2)-10t=50-10
解得:t=3
②若乙在甲的前面,列方程得:
15×2+40(t-2)-10t=50+10
解得:t=![]()
综上,当甲出发3分钟或![]() 分钟时,两人相距10米。
分钟时,两人相距10米。
故答案为:3或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中,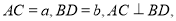 顺次连接四边形
顺次连接四边形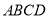 各边中点,得到四边形
各边中点,得到四边形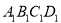 ,再顺次连接四边形
,再顺次连接四边形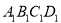 各边中点,得到四边形
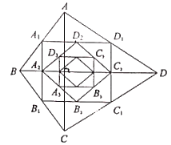
各边中点,得到四边形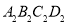 ...如此进行下去,得到四边形
...如此进行下去,得到四边形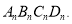 则下列结论正确的个数有( )
则下列结论正确的个数有( )①四边形
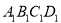 是矩形;②四边形
是矩形;②四边形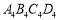 是菱形;③四边形
是菱形;③四边形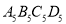 的周长为
的周长为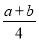 ; ④四边形
; ④四边形 的面积是
的面积是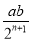 .
.
A.
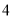 个B.
个B.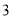 个C.
个C.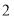 个D.
个D.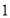 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形
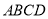 的边
的边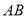 为边作等边三角形
为边作等边三角形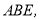 连接
连接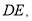 则
则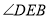 的度数为______.
的度数为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
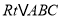 中,
中,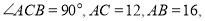 分别以
分别以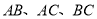 为边在
为边在 的同侧作正方形
的同侧作正方形 ,则图中阴影部分的面积之和为_______.
,则图中阴影部分的面积之和为_______.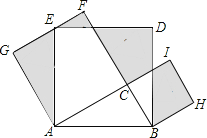
-
科目: 来源: 题型:
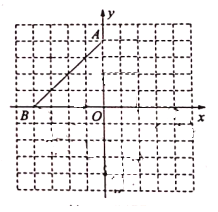
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
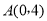 ,点
,点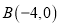 .
.
(1)①画出线段
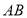 关于
关于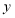 轴对称的线段
轴对称的线段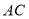 ,则点
,则点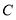 的坐标为 ;
的坐标为 ;②将线段
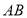 平移至
平移至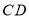 ,其中点
,其中点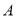 与点
与点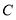 对应,画出线段
对应,画出线段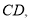 并写出点
并写出点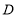 的坐标;
的坐标;(2)点
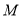 在(1)中四边形
在(1)中四边形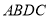 边
边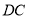 上,且
上,且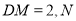 是对角线
是对角线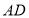 上--动点,则
上--动点,则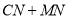 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:等腰三角形中底边与腰的比叫作底角的邻对(can).如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB=
 .容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题: (1) . can30°=______ __;
(2) . 如图②,已知在△ABC中,AB=AC,canB=
 ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
相关试题

