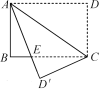
【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
参考答案:
【答案】![]()
【解析】试题分析:根据矩形性质得AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=4-x,AE=4-x,然后在Rt△ABE中利用勾股定理可计算出BE.
试题解析:∵四边形ABCD为矩形,
∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,
∴AE=EC,
设BE=x,则EC=4x,AE=4x,
在Rt△ABE中,∵AB+BE=AE,
∴3+x=(4x) ,解得x=![]() ,
,
即BE的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为
 的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是 .
的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含
 的代数式表示地面的总面积
的代数式表示地面的总面积  ;
;
(2)已知
 ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的  倍,如果铺
倍,如果铺 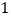 平方米地砖的平均费用为
平方米地砖的平均费用为  元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
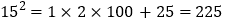 ,
,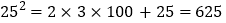 ,
,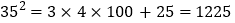 ,…
,…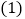 根据上述格式反应出的规律填空:
根据上述格式反应出的规律填空: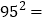 ________;
________; 设这类等式左边两位数的十位数字为
设这类等式左边两位数的十位数字为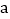 ,请用一个含
,请用一个含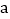 的代数式表示其结果;
的代数式表示其结果;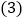 这种简便计算也可以推广应用:个位数字是
这种简便计算也可以推广应用:个位数字是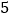 的三位数的平方,请写出
的三位数的平方,请写出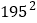 的简便计算过程及结果.
的简便计算过程及结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

-
科目: 来源: 题型:
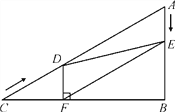
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
相关试题

