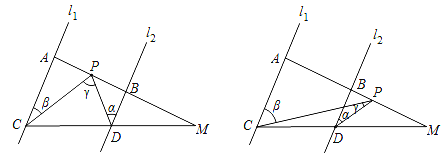
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
参考答案:
【答案】(1)65°;(2)γ=α+β,理由见解析;(3)β﹣α=γ.
【解析】
(1)利用平行线的性质,三角形内角和定理即可证明.
(2)利用平行线的性质,三角形内角和定理即可证明.
(3)利用平行线的性质以及三角形的外角的性质即可解决问题.
(1)∵AC∥BD,
∴β+∠PCD+∠PDC+α=180°,
∵γ+∠PCD+∠PDC=180°,
∴γ=α+β=65°.
(2)∵AC∥BD,
∴β+∠PCD+∠PDC+α=180°,
∵γ+∠PCD+∠PDC=180°,
∴γ=α+β.
(3)如图,当P在B,M之间时,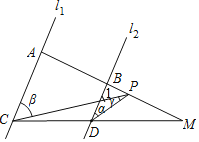
∵AC∥BD,
∴∠1=β,
∵∠1=α+γ,
∴β=α+γ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的直径
的直径 的延长线上,点
的延长线上,点 在
在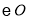 上,
上, 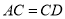 ,
,  ,
,
(1)求证:
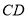 是
是 的切线;
的切线;(2)若
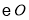 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积. -
科目: 来源: 题型:
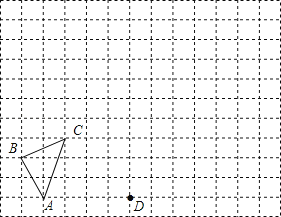
查看答案和解析>>【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(﹣3,0)、(﹣2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(
 取1.73)
取1.73)(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A,B作x轴.y轴的垂线交于点C,如图所示.点P从原点出发,以每秒1个单位长度的速度沿着O→B→C→A的路线移动,运动时间为t秒.
(1)写出A,B,C三点的坐标:A ,B ,C ;
(2)当t=14秒时,求△OAP的面积.
(3)点P在运动过程中,当△OAP的面积为6时,求t的值及点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
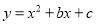 经过A(﹣1,0)、B(3,0)两点.
经过A(﹣1,0)、B(3,0)两点.(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若
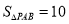 ,求出此时点P的坐标.
,求出此时点P的坐标.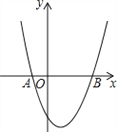
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=a.
(1)AM= ;
(2)如图,以AP为直径作圆,圆心为点C.若⊙C与x轴相切,求a的值;
(3)D是x轴上一点,连接AD、PD.若△OAD∽△BDP,试探究满足条件的点D的个数(直接写出点D的个数及相应a的取值范围,不必说明理由).

相关试题

