【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.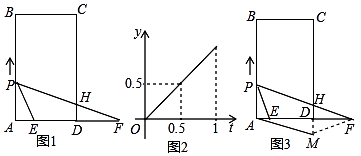
(1)t的取值范围为 , AE=cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
参考答案:
【答案】
(1)0≤t≤3.5;1
(2)
解:如图3,

∵四边形AMHP是菱形,
∴AM=MH=2DM,AM∥PF,
∵∠ADM=90°,DM= ![]() AM,
AM,
∴∠MAD=30°,
∴∠PFA=MFA=∠MAD=30°,
∴MA=MF,
∵MD⊥AF,
∴AD=DF=4,
∴a=4.
(3)
解:当a=4cm时,FA=AD+DF=8cm,
令PA=x,则PF=2x,
根据勾股定理可得,PF2=PA2+AF2,
即(2x)2=x2+82,
解得x= ![]() ,(负值已舍去)
,(负值已舍去)
∴P的运动时间为 ![]() ÷2=
÷2= ![]() 秒
秒
【解析】解:(1)∵AB=7,而7÷2=3.5,
∴0≤t≤3.5,
由题意可知,y= ![]() ×2t×AE,
×2t×AE,
由图2可知,当t=0.5时,y=0.5,
∴0.5= ![]() ×2×0.5×AE,
×2×0.5×AE,
∴AE=1,
故答案分别为:0≤t≤3.5,1;
(1)根据AB的长以及点P的移动速度,可以确定t的范围;根据题意可知,y= ![]() ×2t×AE,由图2可知,当t=0.5时,y=0.5,进而得出0.5=
×2t×AE,由图2可知,当t=0.5时,y=0.5,进而得出0.5= ![]() ×2×0.5×AE,即可求出AE.(2)根据菱形的性质以及轴对称的性质,即可证明∠MAD=∠MFD=30°,最后根据等腰三角形的性质,即可解决问题.(3)令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2 , 即可得出方程(2x)2=x2+82 , 求得x的值即可得到点P的运动时间t.
×2×0.5×AE,即可求出AE.(2)根据菱形的性质以及轴对称的性质,即可证明∠MAD=∠MFD=30°,最后根据等腰三角形的性质,即可解决问题.(3)令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2 , 即可得出方程(2x)2=x2+82 , 求得x的值即可得到点P的运动时间t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
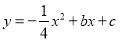 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-3a3)2的结果为( )
A.-9a5B.6a6C.9a6D.6a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3m(2x﹣y)2﹣3mn2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a=355,b=444,c=533,那么a、b、c的大小关系是( )
A. a>b>cB. c>b>aC. b>a>cD. b>c>a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,
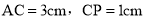 ,求:
,求: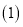 线段AM的长;
线段AM的长;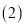 线段PN的长.
线段PN的长.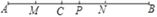
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2
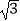 ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( ) 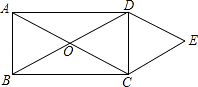
A.2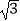
B.4
C.4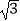
D.8
相关试题

