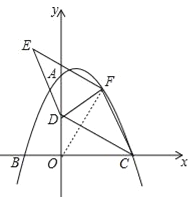
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).

(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
参考答案:
【答案】(1)![]() ,C(8,0);(2)①50;②18.
,C(8,0);(2)①50;②18.
【解析】
试题分析:(1)把A点和B点坐标代入![]() 得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
(2)①连结OF,如图,设F(t,![]() ),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=
),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=![]() ,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),然后把E(t﹣8,
),然后把E(t﹣8,![]() )代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
试题解析:(1)把A(0,8),B(﹣4,0)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,所以抛物线的解析式为
,所以抛物线的解析式为![]() ;
;
当y=0时,![]() ,解得
,解得![]() ,
,![]() ,所以C点坐标为(8,0);
,所以C点坐标为(8,0);
(2)①连结OF,如图,设F(t,![]() ),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=
),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=![]() =
=![]() =
=![]() ;
;
当t=3时,△CDF的面积有最大值,最大值为25,∵四边形CDEF为平行四边形,∴S的最大值为50;
②∵四边形CDEF为平行四边形,∴CD∥EF,CD=EF,∵点C向左平移8个单位,再向上平移4个单位得到点D,∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),∵E(t﹣8,
),∵E(t﹣8,![]() )在抛物线上,∴
)在抛物线上,∴ ![]() ,解得t=7,当t=7时,S△CDF=
,解得t=7,当t=7时,S△CDF=![]() =9,∴此时S=2S△CDF=18.
=9,∴此时S=2S△CDF=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,若∠1与∠2 是同旁内角,且∠1=70,则 ( )
A. ∠2=70B. ∠2=110
C. ∠2=70或∠2=110D. ∠2的度数不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x=x3B.(﹣2x2)3=8x5
C.(x+1)(x﹣2)=x2﹣x﹣2D.(x﹣y)2=x2﹣y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有6名同学参加校“综合素质技能竞赛”,成绩(单位:分)分别是87,92,87,91,94,76.则他们成绩的中位数是_____分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-3a3)2的结果为( )
A.-9a5B.6a6C.9a6D.6a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3m(2x﹣y)2﹣3mn2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.
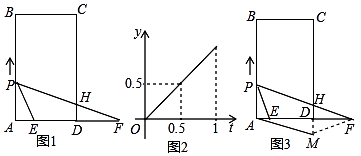
(1)t的取值范围为 , AE=cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
相关试题

