【题目】如图,互相垂直的两条射线OE与OF的端点O在三角板的内部,与三角板两条直角边的交点分别为点D、B.
(1)填空:若∠ABO=50°,则∠ADO= ;
(2)若DC、BP分别是∠ADO、∠ABF的角平分线,如图1.求证:DC⊥BP;
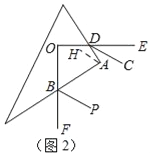
(3)若DC、BP分别分别是∠ADE、∠ABF的角平分线,如图2.猜想DC与BP的位置关系,并说明理由.
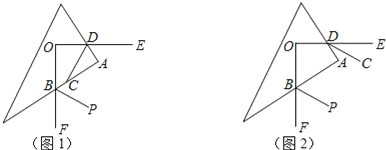
参考答案:
【答案】(1)130°;(2)证明见解析,(3)DC与BP互相平行.理由见解析.
【解析】试题分析:(1)由四边形的内角和为360°即可得;
(2)如图1,延长DC交BP于G,由∠OBA+∠ODA=180°、∠OBA+∠ABF=180°可得∠ODA=∠ABF,再由DC、BP分别是∠ADO、∠ABF的角平分线,从而可得∠CDA=∠CBG,再由∠DCA=∠BCG,继而可得∠BGC=∠A=90°,即得DC⊥BP;
(3)DC与BP互相平行.如图2,作过点A作AH∥BP,则可得∠ABP=∠BAH,由∠OBA+∠ODA=180°,可得∠ABF+∠ADE=180°,再由DC、BP分别分别是∠ADE、∠ABF的角平分线,从而可得∠ADC+∠ABP=90°,进而可得∠DAH=∠ADC,从而可得CD∥AH,最后得CD∥BP.
试题解析:(1)如图1,∵OE⊥OF,∴∠EOF=90°,
在四边形OBAD中,∠A=∠BOD=90°,∠ABO=50°,
∴∠ADO=360°﹣90°﹣90°﹣50°=130°;
故答案为:130°;
(2)如图1,延长DC交BP于G,
∵∠OBA+∠ODA=180°,而∠OBA+∠ABF=180°,∴∠ODA=∠ABF,
∵DC、BP分别是∠ADO、∠ABF的角平分线,∴∠CDA=∠CBG,
而∠DCA=∠BCG,∴∠BGC=∠A=90°,∴DC⊥BP;

(3)DC与BP互相平行.
理由:如图2,作过点A作AH∥BP,则∠ABP=∠BAH,
∵∠OBA+∠ODA=180°,∴∠ABF+∠ADE=180°,
∵DC、BP分别分别是∠ADE、∠ABF的角平分线,∴∠ADC+∠ABP=90°,
∴∠ADC+∠BAH=90°,
而∠DAH+∠BAH=90°,∴∠DAH=∠ADC,∴CD∥AH,∴CD∥BP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校于“三八”妇女节期间组织女教师到横店影视城旅游.下面是领队与旅行社导游收费标准的一段对话:
【领队】组团去横店影视城旅游每人收费是多少?
【导游】如果人数不超过30人,人均旅游费用为360元.
【领队】超过30人怎样优惠呢?
【导游】如果超过30人,每增加1人,人均旅游费用降低5元,但人均旅游费用不得低于300元.
该学校按旅行社的收费标准组团浏览横店影视城结束后,共支付给旅行社12400元.设该学校这次参加旅游的女教师共有
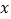 人.
人.请你根据上述信息,回答下列问题:
(1)该学校参加旅游的女教师人数x的取值范围是 ;
(2)该学校参加旅游的女教师每人实际应收费 元(用含x的代数式表示);
(3)求该学校这次到横店影视城旅游的女教师共有多少人?
-
科目: 来源: 题型:
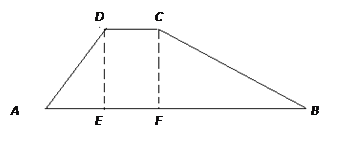
查看答案和解析>>【题目】水库大坝截面的迎水坡坡比(DE与AE的长度之比)为5:3,背水坡坡比为1:2,大坝高DE=30m,坝顶宽CD=10m,求大坝的截面的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)
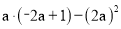 (2)
(2) 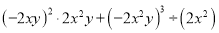
(3)
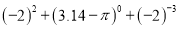 (4)
(4) 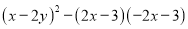
(5)
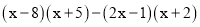 (6)
(6) 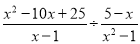
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x﹣1)(x+2)=0的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay
B.x2+2x+1=x(x+2)+1
C.(x+1)(x+3)=x2+4x+3
D.x3﹣x=x(x+1)(x﹣1) -
科目: 来源: 题型:
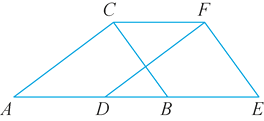
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出BE的长度.
相关试题

