搜索
【题目】如图，矩形纸片ABCD，AD=4，AB=3，如果点E在边BC上，将纸片沿AE折叠，使点B落在点F处，联结FC，当△EFC是直角三角形时，那么BE的长为_____．
参考答案：
【答案】1.5或3
【解析】根据矩形的性质，利用勾股定理求得AC=
=5，由题意，可分△EFC是直角三角形的两种情况：
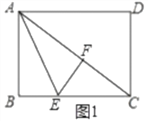
如图1，当∠EFC=90°时，由∠AFE=∠B=90°，∠EFC=90°，可知点F在对角线AC上，且AE是∠BAC的平分线，所以可得BE=EF，然后再根据相似三角形的判定与性质，可知△ABC∽△EFC，即
，代入数据可得
，解得BE=1.5；
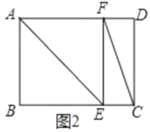
如图2，当∠FEC=90°，可知四边形ABEF是正方形，从而求出BE=AB=3.
故答案为：1.5或3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是2015年12月月历．
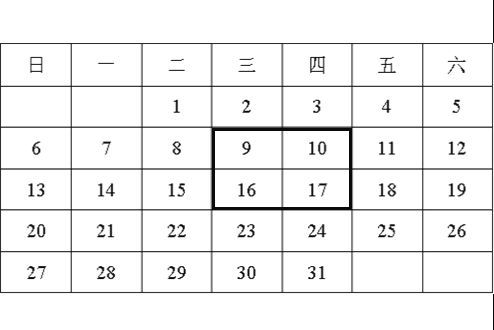
（1）如图，用一正方形框在表中任意框往4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是 ， ， ．
（2）在表中框住四个数之和最小记为a1，和最大记为a2，则a1+a2= ．
（3）当（1）中被框住的4个数之和等于76时，x的值为多少？
（4）在（1）中能否框住这样的4个数，它们的和等于92？若能，则求出x的值；若不能，则说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC，垂足为D，AD=CD，点E在AD上，DE=BD，M、N分别是AB、CE的中点．
（1）求证：△ADB≌△CDE；
（2）求∠MDN的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE，连接BE，延长DE、BC相交于点F，则有∠BFE=90°，且四边形ACFD是一个正方形．
（1）判断△ABE的形状，并证明你的结论；
（2）用含b代数式表示四边形ABFE的面积；
（3）求证：a2+b2=c2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面上有四个点A，B，C，D．
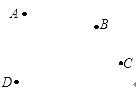
（1）根据下列语句画图:
①射线BA；
②直线AD，BC相交于点E；
③延长DC至F（虚线），使CF=BC，连接EF（虚线）．
（2）图中以E为顶点的角中，小于平角的角共有__________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，画
，并画
的平分线
．（1）将三角尺的直角顶点落在
的任意一点P上，使三角尺的两条直角边与的两边分别垂直，垂足为E、F（如图1），则
（选填＜，＞，＝）
（2）把三角尺绕着点P旋转（如图2），
与相等吗？试猜想、的大小关系，并说明理由．拓展延伸1：在（2）条件下，过点P作直线
，分别交
、
于点G、H，如图3①图中全等三角形有多少对（不添加辅助线）
②猜想
、
、
之间的关系，并证明你的猜想．拓展延伸2：
画
，并画的平分线，在上任取一点P，作
．
的两边分别与、相交于E、F两点（如图4），与相等吗？请说明理由． -
科目： 来源： 题型：
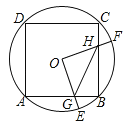
查看答案和解析>>【题目】（2016湖北省咸宁市）如图，边长为4的正方形ABCD内接于点O，点E是
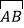上的一动点（不与A、B重合），点F是
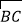上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论：①
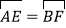；②△OGH是等腰三角形；
③四边形OGBH的面积随着点E位置的变化而变化；
④△GBH周长的最小值为
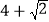．其中正确的是________（把你认为正确结论的序号都填上）．
相关试题
