【题目】如图,画![]() ,并画
,并画![]() 的平分线
的平分线![]() .
.
(1)将三角尺的直角顶点落在![]() 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与![]() 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则![]()
![]() (选填<,>,=)
(选填<,>,=)

(2)把三角尺绕着点P旋转(如图2),![]() 与
与![]() 相等吗?试猜想
相等吗?试猜想![]() 、
、![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
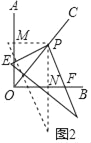
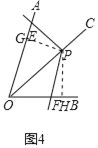
拓展延伸1:在(2)条件下,过点P作直线![]() ,分别交
,分别交![]() 、
、![]() 于点G、H,如图3
于点G、H,如图3
①图中全等三角形有多少对(不添加辅助线)
②猜想![]() 、
、![]() 、
、![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.
拓展延伸2:
画![]() ,并画
,并画![]() 的平分线
的平分线![]() ,在
,在![]() 上任取一点P,作
上任取一点P,作![]() .
.![]() 的两边分别与
的两边分别与![]() 、
、![]() 相交于E、F两点(如图4),
相交于E、F两点(如图4),![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
参考答案:
【答案】(1)=;(2)![]() ,理由见解析;拓展延伸1:①全等三角形有3对;②
,理由见解析;拓展延伸1:①全等三角形有3对;②![]() ,理由见解析;拓展延伸2:
,理由见解析;拓展延伸2:![]() ;理由见解析;
;理由见解析;
【解析】
(1)根据角平分线的性质定理证明;
(2)证明△MPE≌△NPF,根据全等三角形的性质证明结论;
拓展延伸1:①根据等腰直角三角形的性质得到OP=PG=PH,证明△GPE≌△OPF(ASA),△EPO≌△FPH,△GPO≌△OPH,得到答案;
②根据勾股定理,全等三角形的性质解答;
拓展延伸2:作PG⊥OA于G,PH⊥OB于H,证明△PGE≌△PHF,根据全等三角形的性质证明结论.
(1)∵![]() 平分
平分![]() ,
,
∴![]() ,
,
故答案为:=;
(2)![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
由(1)得,![]() ,
,
在![]() 和
和![]() 中,
中,
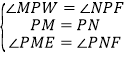 ,
,
∴![]() ,
,
∴![]() ;
;
拓展延伸1:①∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵GH⊥OC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
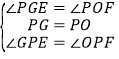 ,
,
∴![]() ,
,
同理,![]() ,
,
故答案为:3;
②![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ;
;
拓展延伸2:![]() ;
;
理由:作![]() 于G,
于G,![]() 于H,
于H,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
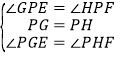 ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线m与直线n相交于点O,A、B两点同时从点O出发,点A以每秒x个单位长度沿直线n向左运动,点B以每秒y个单位长度沿直线m向上运动。
(1)若运动1s时,点B比点A多运动1个单位;运动2s时,点B与点A运动的路程和为6个单位,则x=_________,y=___________.
(2)如图,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.在点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.
(3)如图,将(2)中的直线n不动,直线m绕点O按顺时针方向旋转α(0<ɑ<90),其他条件不变.ⅰ)用含有α的式子表示∠APB的度数____________.
ⅱ)如果再分别作△ABO的两个外角∠BAC,∠ABD的角平分线相交于点Q,并延长BP、QA交于点M.则下列结论正确的是___________(填序号) .
①APB与∠Q互补;②∠Q与∠M互余;③∠APB-∠M为定值;④∠M-∠Q为定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 的平分线相交于点D,
的平分线相交于点D, 过点D且
过点D且 ,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长__.
,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格纸中,点A、B、C在小正方形的顶点上.
(1)求
 的面积;
的面积;(2)在图中画出与
 关于直线1成轴对称的
关于直线1成轴对称的 ;
;(3)在如图所示网格纸中,以
 为一边作与
为一边作与 全等的三角形,可以作出多少个三角形与
全等的三角形,可以作出多少个三角形与 全等(不要超出网格纸的范围).
全等(不要超出网格纸的范围).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①有一个角是
 的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )A.
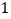 个B.
个B. 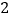 个C.
个C. 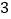 个D.
个D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
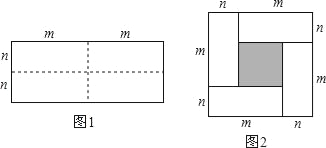
(1)直接写出图2中的阴影部分面积;
(2)观察图2,请直接写出下列三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
相关试题

