【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.


参考答案:
【答案】(1)30°
(2)![]() cm
cm
【解析】
(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30
∵纸带宽为15,∴sin∠DAB=sin∠ABM=![]() ,∴∠DAB=30°.
,∴∠DAB=30°.
(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,

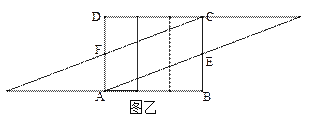
将图甲种的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图乙中的□ABCD,
此平行四边形即为图2中的□ABCD
由题意得,知:BC=BE+CE=2CE=2×![]() ,
,
∴所需矩形纸带的长为MB+BC=30·cos30°+![]() =
=![]() cm.
cm.
-
科目: 来源: 题型:
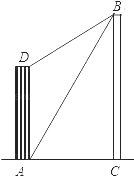
查看答案和解析>>【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.

(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r . -
科目: 来源: 题型:
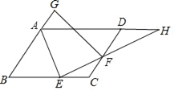
查看答案和解析>>【题目】如图所示,在ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD于F.
(1)求证:CE=CF;
(2)延长AD、EF交于点H,延长BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的长.
-
科目: 来源: 题型:
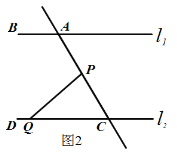
查看答案和解析>>【题目】如图1,点A、B在直线
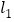 上,点C、D在直线
上,点C、D在直线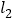 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,∠EAC+∠ACE=90° .
(1)请判断
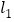 与
与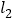 的位置关系并说明理由;
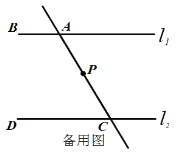
的位置关系并说明理由;(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
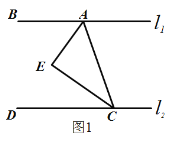
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠AOE=∠GOD.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
相关试题

