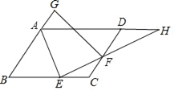
【题目】如图所示,在ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD于F.
(1)求证:CE=CF;
(2)延长AD、EF交于点H,延长BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的长.
参考答案:
【答案】(1)见解析;(2)GF=4![]() .
.
【解析】
(1)由题意可得:∠DAE=∠BAE=∠AEB=![]() ∠BAD=
∠BAD=![]() ∠C,则
∠C,则![]() ∠C+∠FEC=90°,根据三角形内角和可得
∠C+∠FEC=90°,根据三角形内角和可得![]() ∠C+∠EFC=90°,则∠CEF=∠CFE,即可得结论;
∠C+∠EFC=90°,则∠CEF=∠CFE,即可得结论;
(2)连接AC,作AP⊥BC于P,由题意可求AB=BE=CD=5,CE=CF=2,即可求DH=3,根据勾股定理可求AE的长,根据勾股定理可列出方程,可求出 BP,AP,PE,PC的长度,再根据勾股定理可求AC的长,由题意可证AC=GF,即可得GF的长.
(1)∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠BAE=∠DAE=![]() ∠BAD,
∠BAD,
∴∠BAE=∠AEB=![]() ∠BAD,
∠BAD,
∴AB=BE,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠FEC=90°,即![]() ∠BAD+∠FEC=90°,
∠BAD+∠FEC=90°,
∴![]() ∠C+∠FEC=90°,
∠C+∠FEC=90°,
∵∠C+∠FEC+∠EFC=180°,
∴![]() ∠C+∠EFC=90°,
∠C+∠EFC=90°,
∴∠EFC=∠FEC,
∴CE=CF;
(2)如图连接AC,作AP⊥BC于P,
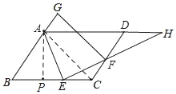
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=7,AB∥CD,
∵CE=CF,
∴BC﹣BE=CD﹣DF,且AB=BE=CD,
∴7﹣AB=AB﹣3,
∴AB=5=BE=CD,
∴CE=CF=2,
∵AD∥BC,
∴∠H=∠FEC,且∠FEC=∠EFC,∠DFH=∠EFC,
∴∠H=∠DFH,
∴DH=DF=3,
∴AH=10,
在Rt△AEH中,AH2=AE2+EH2,且EH=2AE,
∴5AE2=100,
∴AE=2![]() ,
,
在Rt△ABP和Rt△APE中,
AP2=AB2﹣BP2,AP2=AE2﹣PE2.
∴AB2﹣BP2=AE2﹣PE2.
∴25﹣BP2=20﹣(5﹣BP)2.
∴BP=3,
∴AP=4,PE=2,PC=4,
在Rt△APC中,AC=![]() =4
=4![]() ,
,
∵AB∥CD,AG=CF,
∴四边形AGFC是平行四边形,
∴GF=AC=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.

(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式. -
科目: 来源: 题型:
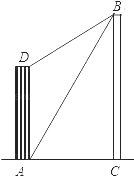
查看答案和解析>>【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.

(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.



-
科目: 来源: 题型:
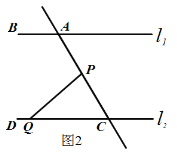
查看答案和解析>>【题目】如图1,点A、B在直线
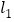 上,点C、D在直线
上,点C、D在直线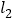 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,∠EAC+∠ACE=90° .
(1)请判断
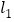 与
与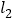 的位置关系并说明理由;
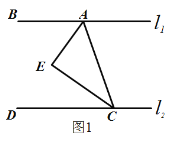
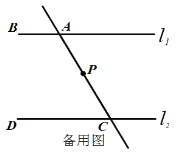
的位置关系并说明理由;(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

相关试题

