【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.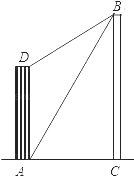
参考答案:
【答案】解:过点B作BE⊥AD,交AD延长线于点E.
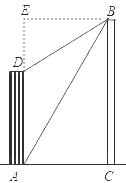
在Rt△BED中,∵D点测得塔顶B点的仰角为30°,
∴∠BDE=60度.
设DE=x,则BE= ![]() x.
x.
在Rt△BEA中,∠BAE=30度,BE= ![]() x.
x.
∴AE=3x.
∴AD=AE-DE=3x-x=2x=10.
∴x=5.
∴BC=AD+DE=10+5=15(米).
答:塔BC的高度为15米.
【解析】根据题意画出图形,由D点测得塔顶B点的仰角为30°,根据在直角三角形中,30度角所对的边是斜边的一半;求出塔BC的高度.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%

(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装着5个完全相同的小球,分别标有数字0,1,,2,-1,-2,从袋中随机取出一个小球。
(1)随机地从布袋中摸出一个小球,则摸出的球上数字为正数的概率为
(2)若第一次从布袋中随机摸出一个小球,设记下的数字为x,再将此球放回盒中,第二次再从布袋中随机抽取一张,设记下的数字为y,记M(x,y),请用画树状图或列表法列举出点M所有可能的坐标,并求点M位于第二象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.

(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.

(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r . -
科目: 来源: 题型:
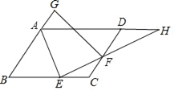
查看答案和解析>>【题目】如图所示,在ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD于F.
(1)求证:CE=CF;
(2)延长AD、EF交于点H,延长BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.



相关试题

