【题目】如图,在矩形ABCD中,AD= ![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;
②OE=OD;
③BH=HF;
④BC﹣CF=2HE;
⑤AB=HF.
其中正确的有( )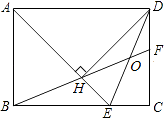
A.①②③④⑤
B.①②③④
C.①③④⑤
D.①②③⑤
参考答案:
【答案】B
【解析】解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE= ![]() AB,
AB,
∵AD= ![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,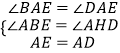
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB= ![]() (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,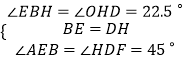
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A. 增加(n﹣2)×180° B. 减小(n﹣2)×180° C. 增加(n﹣1)×180° D. 没有改变
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程x2﹣4mx+m2=0的一个根,代数式m(m﹣8)﹣1的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果只用一种正多边形做平面密铺,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的每个内角度数为______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.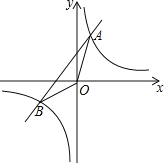
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式
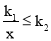 x+b的解.
x+b的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣2x=0
(2)(x﹣3)2=(2x﹣1)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】十九大报告中提出“广泛开展全民健身活动,加快推进体育强国建设”.为了响应号召,提升学生训练兴趣,某中学自编“功夫扇”课间操.若设最外侧两根大扇骨形成的角为∠COD,当“功夫扇”完全展开时∠COD=160°.在扇子舞动过程中,扇钉O始终在水平线AB上.
小华是个爱思考的孩子,不但将以上实际问题抽象为数学问题,而且还在抽象出的图中画出了∠BOC 的平分线OE,以便继续探究.
(1)当扇子完全展开且一侧扇骨OD呈水平状态时,如图1所示.请在抽象出的图2中画出∠BOC 的平分线OE,此时∠DOE的度数为 ;

(2)“功夫扇”课间操有一个动作是把扇子由图1旋转到图3所示位置,即将图2中的∠COD绕点O旋转至图4所示位置,其他条件不变,小华尝试用如下两种方案探究了∠AOC和∠DOE度数之间的关系.

方案一:设∠BOE的度数为x.
可得出
 ,则
,则 .
. ,则
,则 .
.进而可得∠AOC和∠DOE度数之间的关系.
方案二:如图5,过点O作∠AOC的平分线OF.

易得
 ,即
,即 .
.由
 ,可得
,可得 .
.进而可得∠AOC和∠DOE度数之间的关系.
参考小华的思路可得∠AOC和∠DOE度数之间的关系为 ;
(3)继续将扇子旋转至图6所示位置,即将∠COD绕点O旋转至如图7所示的位置,其他条件不变,请问(2)中结论是否依然成立?说明理由.

相关试题

