【题目】十九大报告中提出“广泛开展全民健身活动,加快推进体育强国建设”.为了响应号召,提升学生训练兴趣,某中学自编“功夫扇”课间操.若设最外侧两根大扇骨形成的角为∠COD,当“功夫扇”完全展开时∠COD=160°.在扇子舞动过程中,扇钉O始终在水平线AB上.
小华是个爱思考的孩子,不但将以上实际问题抽象为数学问题,而且还在抽象出的图中画出了∠BOC 的平分线OE,以便继续探究.
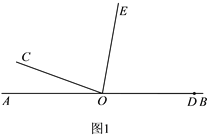
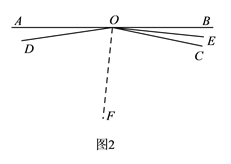
(1)当扇子完全展开且一侧扇骨OD呈水平状态时,如图1所示.请在抽象出的图2中画出∠BOC 的平分线OE,此时∠DOE的度数为 ;

(2)“功夫扇”课间操有一个动作是把扇子由图1旋转到图3所示位置,即将图2中的∠COD绕点O旋转至图4所示位置,其他条件不变,小华尝试用如下两种方案探究了∠AOC和∠DOE度数之间的关系.

方案一:设∠BOE的度数为x.
可得出![]() ,则
,则![]() .
.
![]() ,则
,则![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
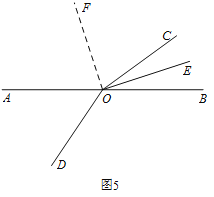
方案二:如图5,过点O作∠AOC的平分线OF.

易得![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
参考小华的思路可得∠AOC和∠DOE度数之间的关系为 ;
(3)继续将扇子旋转至图6所示位置,即将∠COD绕点O旋转至如图7所示的位置,其他条件不变,请问(2)中结论是否依然成立?说明理由.

参考答案:
【答案】(1)80°;(2)![]() ;(3)不成立
;(3)不成立
【解析】试题分析:(1)根据题意画出角平分线,然后根据角平分线的定义进行求解即可;
(2)结合图形完成题中所给两个方案的过程即可得;
(3)不成立,按(2)中的两个方案进行验证即可得.
试题解析:(1)如图1,
∵OE平分∠COD,∠COD=160°,
∴∠DOE=![]() ∠COD=80°,
∠COD=80°,
故答案为:80°;
(2)方案一:设∠BOE的度数为x,
∵OE平分∠BOC,∴∠BOC=2∠BOE=2x,
∴![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
,
∴![]() =
= ![]() ,
,
∴![]() ;
;
方案二:如图5,过点O作∠AOC的平分线OF,
∵OE平分∠BOE,OF平分∠AOC,∴∠COE=![]() ∠BOC,∠COF=
∠BOC,∠COF=![]() ∠AOC,
∠AOC,
∵∠AOC+∠BOC=180°,∴∠COE+∠COF=90°,即![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
故答案为: ![]() ;
;
(3)不成立.
理由如下:
方法一:设∠BOE的度数为x.
可得出![]() ,则
,则![]() .
.
![]() ,则
,则![]() .
.
所以![]() .
.
方法二:如图2,过点O作∠AOC的平分线OF.
易得![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=
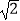 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;
②OE=OD;
③BH=HF;
④BC﹣CF=2HE;
⑤AB=HF.
其中正确的有( )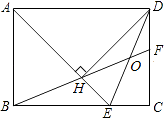
A.①②③④⑤
B.①②③④
C.①③④⑤
D.①②③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
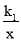 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.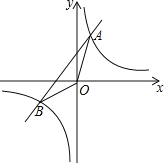
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式
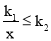 x+b的解.
x+b的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣2x=0
(2)(x﹣3)2=(2x﹣1)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,AB=CD=10cm,BC=AD=8cm,动点P以1cm/s的速度从A点出发,沿A→B→C→D路线运动到点D停止,动点Q以2cm/s的速度从D点出发,沿D→C→B→A路线运动到点A停止,两点同时出发,6s后P、Q同时改变速度,点P的速度为2cm/s,点Q的速度为1cm/s, 当点Q出发_____秒时,点P与点Q在运动路线上相距的路程为26cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ______ ;扇形统计图中的圆心角α等于 ______ ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】剧院里5排2号可以用(5,2)表示,那么3排7号可以用________表示.
相关试题

