【题目】我们把对角线互相垂直的四边形叫做垂美四边形.
(1)(概念理解)在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是___________.
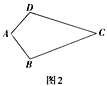
(2)(性质探究)如图2,试探索垂美四边形ABCD的两组对边AB,CD与BC ,AD之间的数量关系,写出证明过程。
(3)(问题解决)如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE,连接CE,BG,GE, 已知AC=![]() ,BC=1 求GE的长.
,BC=1 求GE的长.

参考答案:
【答案】菱形、正方形
【解析】(1)根据垂美四边形的定义进行判断即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.
(1)菱形的对角线互相垂直,符合垂美四边形的定义,
正方形的对角线互相垂直,符合垂美四边形的定义,
而平行四边形、矩形的对角线不一定垂直,不符合垂美四边形的定义,
故答案为:菱形、正方形;
(2)猜想结论:AD2+BC2=AB2+CD2,证明如下:
如图2,连接AC、BD,交点为E,则有AC⊥BD,
∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2;
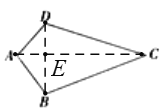
(3)连接CG、BE,设AB与CE的交点为M
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
又∠AEC+∠AME=90°,∠AME=∠BMC,
∴∠ABG+∠BMC=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=![]() ,BC=1 ∴AB=2,
,BC=1 ∴AB=2,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
GE的长是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一学校(点M)距公路(直线l)的距离(MA)为1km,在公路上距该校2km处有一车站(点N),该校拟在公路上建一个公交车停靠点(点p),以便于本校职工乘车上下班,要求停靠站建在AN之间且到此校与车站的距离相等,请你计算停靠站到车站的距离.
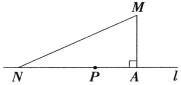
-
科目: 来源: 题型:
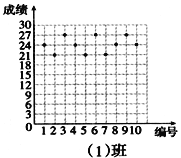
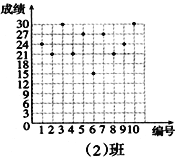
查看答案和解析>>【题目】王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年(1)班和八年(2)班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
班级
平均分(分)
中位数(分)
众数(分)
八年(1)班
24
24
八年(2)班
24
(2)你认为那个班的学生纠错的得分情况比较整齐一些,通过计算说明理由.
-
科目: 来源: 题型:
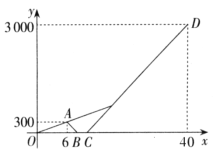
查看答案和解析>>【题目】为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6min发现忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前走,小亮取回借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆。已知骑车的速度是步行速度的2倍,如图是小亮和姐姐距离家的路程y(m)与出发的时间x(min)的函数图象,根据图象解答下列问题:
(1)小亮在家停留了多长时间?
(2)求小亮骑车从家出发去图书馆时距家的路程 y(m)与出发时间 x(min)之间的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明想探究函数
 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…
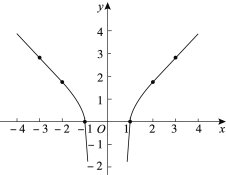
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数
 的一条性质:_____________.
的一条性质:_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
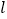 的表达式为
的表达式为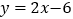 ,点A,B的坐标分别为
,点A,B的坐标分别为(1,0),(0,2),直线AB与直线
 相交于点P.
相交于点P.(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线
 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.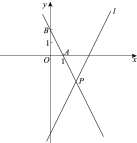
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下表三行数的规律,回答下列问题:
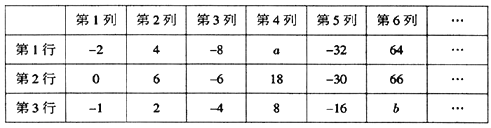
(1)第1行的第四个数a是多少;第3行的第六个数b是多少;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为多少;
(3)巳知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
相关试题

