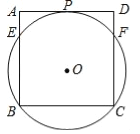
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
(1)求证:PF平分∠BFD.
(2)若tan∠FBC=![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据切线的性质得到OP⊥AD,由四边形ABCD的正方形,得到CD⊥AD,推出OP∥CD,根据平行线的性质得到∠PFD=∠OPF,由等腰三角形的性质得到∠OPF=∠OFP,根据角平分线的定义即可得到结论;(2)由∠C=90°,得到BF是⊙O的直径,根据圆周角定理得到∠BEF=90°,推出四边形BCFE是矩形,根据矩形的性质得到EF=BC,根据切割线定理得到PD2=DFCD,于是得到结论.
试题解析:(1)连接OP,BF,PF,
∵⊙O与AD相切于点P,
∴OP⊥AD,
∵四边形ABCD的正方形,
∴CD⊥AD,
∴OP∥CD,
∴∠PFD=∠OPF,
∵OP=OF,
∴∠OPF=∠OFP,
∴∠OFP=∠PFD,
∴PF平分∠BFD;
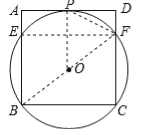
(2)连接EF,
∵∠C=90°,
∴BF是⊙O的直径,
∴∠BEF=90°,
∴四边形BCFE是矩形,
∴EF=BC,
∵AB∥OP∥CD,BO=FO,
∴OP=![]() AD=
AD=![]() CD,
CD,
∵PD2=DFCD,即(![]() )2=
)2=![]() CD,
CD,
∴CD=4![]() ,
,
∴EF=BC=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用提公因式法分解因式:
(1)6m2n-15n2m+30m2n2;
(2)-4x3+16x2-26x;
(3)x(x+y)+y(x+y). -
科目: 来源: 题型:
查看答案和解析>>【题目】用提公因式法进行简便计算:
(1)30.14×950+30.14×50;
(2)3.14×31+27×3.14+42×3.14. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2
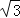 ,求ABCD的面积.
,求ABCD的面积.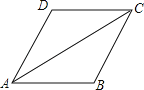
-
科目: 来源: 题型:
查看答案和解析>>【题目】确定下列多项式中各项的公因式:
(1)2x2+6x3;
(2)5(a-b)3+10(a-b). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的是( )
A. 2a+5b=7ab B. 4+5x=9x C. -3(x2-4)=-3x2+4 D. 2-3x=-(3x-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题有( )
①对角线互相平分的四边形是平行四边形;
②两组对角分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个
B.2个
C.1个
D.0个
相关试题

