【题目】如图, ![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证: ![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

参考答案:
【答案】(1)证明见解析;(2)存在, DE=2![]() cm;(3)存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
cm;(3)存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
【解析】试题分析:
(1)由旋转的性质结合△ABC是等边三角形可得∠DCB=60°,CD=CE,从而可得△CDE是等边三角形;
(2)由(1)可知△CDE是等边三角形,由此可得DE=CD,因此当CD⊥AB时,CD最短,则DE最短,结合△ABC是等边三角形,AC=4即可求得此时DE=CD=![]() ;
;
(3)由题意需分0≤t<6,6<t<10和t>10三种情况讨论,①当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,由此可知:此时若△DBE是直角三角形,则∠BED=90°;②当6<t<10s时,由性质的性质可知∠DBE=120°>90°,由此可知:此时△DBE不可能是直角三角形;③当t>10s时,由旋转的性质可知,∠DBE=60°,结合∠CDE=60°可得∠BDE=∠CDE+∠BDC=60°+∠BDC>60°,由此可得∠BED<60°,由此可知此时若△BDE是直角三角形,则只能是∠BDE=90°;这样结合已知条件即可分情况求出对应的t的值了.
试题解析:
(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)存在,当6<t<10时,
由(1)知,△CDE是等边三角形,
∴DE=CD,
由垂线段最短可知,当CD⊥AB时,CD最小,
此时∠ADC=90°,又∵∠ACD=60°,
∴∠ACD=30°,
∴ AD=![]() AC=2,
AC=2,
∴ CD=![]() ,
,
∴ DE=2![]() (cm);
(cm);

(3)存在,理由如下:
①当0s≤t<6s时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴此时若△DBE是直角三角形,则∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEC=60°,
∴∠CEB=∠BED-∠DEC=30°,
∴∠CDA=∠CEB=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA﹣DA=6﹣4=2,
∴t=2÷1=2(s);
②当6s<t<10s时,由性质的性质可知∠DBE=120°>90°,
∴此时△DBE不可能是直角三角形;
③当t>10s时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14cm,
∴t=14÷1=14(s);
综上所述:当t=2s或14s时,以D、E、B为顶点的三角形是直角三角形.
-
科目: 来源: 题型:
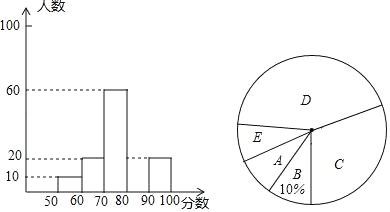
查看答案和解析>>【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A
50<n≤60
B
60<n≤70
C
70<n≤80
D
80<n≤90
E
90<n≤100
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.
(1)篮球和排球各购进了多少个(列方程组解答)?
(2)因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:
①旋转角是____度;
②线段OD的长为_____;
③求∠BDC的度数.
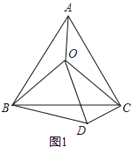
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,∠A0B=135,OA=1,0B=2,求0C的长.
小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.

-
科目: 来源: 题型:
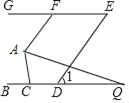
查看答案和解析>>【题目】如图,已知BC∥GE,AF∥DE,∠1=56°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=14°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )
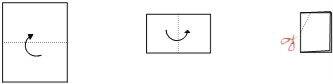
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形各个内角的平分线围成一个四边形,则这个四边形一定是( )
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
相关试题

