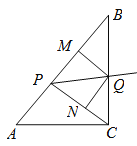
【题目】如图,已知,在Rt ![]() 中,斜边
中,斜边![]() ,
, ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分
,点P为边AB上一动点(不与A,B重合),PQ平分![]() 交边BC于点Q,
交边BC于点Q, ![]() 于
于![]() 于N.
于N.
(1)当AP=CP时,求![]() ;
;
(2)若![]() ,求CQ;
,求CQ;
(3)探究:AP为何值时,四边形PMQN与![]() 的面积相等?
的面积相等?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 时,四边形PMQN与
时,四边形PMQN与![]() 的面积相等
的面积相等
【解析】分析:(1)由PQ为平分线,AP=CP,可得:PQ∥AC,再由AC⊥BC,PQ⊥BC,可得∠PCQ=∠PBQ即PC=PB,即可解出.(2)由△ABC的面积可得出PC的长,再由勾股定理列方程求出PB的长,MQ//PC推出 △BMQ∽△BPC,根据相似三角形性质解出结果;(3)(3)根据四边形PMQN和三角形△BPQ的面积相等得到QM是BP的垂直平分线,再由△CPQ∽△CBP即可作答.
本题解析:(1)在Rt ![]() 中,斜边
中,斜边![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() ,
, ![]()
又∵PQ是∠BPC的平分线,
![]() ∴
∴![]()
又∵![]() ,
,![]()
![]() 为
为![]() 中点,
中点, ![]()
(2)![]() ,
,
![]()
![]() 得:
得: ![]() ,
,
设![]() 由勾股定理可列方程:
由勾股定理可列方程: ![]() ,
,
解得: ![]()
又![]()
![]() ,
,![]()
![]() ,
, ![]()
(3)由角平分线性质易得![]() ,
, ![]() ,
,
![]() 即
即![]() .∴QM是BP的垂直平分线,
.∴QM是BP的垂直平分线,
∴∠QPB=∠PBQ.∵∠QPB=∠CPQ∴∠PBQ=∠CPQ.
又∵∠PCQ=∠BCP,∴![]() .
.
![]() ,
,
![]() ,得
,得![]()
再由![]() 式得
式得![]() ,
,
![]() ,
,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A组数据如下:0,1,-2,-1,0,-1,3
(1)求A组数据的平均数;
(2)从A组数据中选取5个数据,记这5个数据为B组数据,要求B组数据满足两个条件:①它的平均数与A组数据的平均数相等;②它的方差比A组数据的方差大.
请你选取B组的数据,并请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.

(1)求证:AB∥CD;
(2)H是直线CD上一动点(不与点D重合),BI平分∠HBD.写出∠EBI与∠BHD的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(a,﹣a),点B坐标为(b,c),a,b,c满足
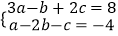 .
.
(1)若a没有平方根,判断点A在第几象限并说明理由;
(2)若点A到x轴的距离是点B到x轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,﹣2),△OAB的面积是△DAB面积的2倍,求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=3x+1的图象沿y轴向下平移2个单位长度,所得直线的函数表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
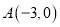 ,二次函数
,二次函数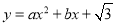 的对称轴为直线
的对称轴为直线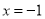 ,其图象过点
,其图象过点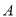 与
与 轴交于另一点
轴交于另一点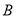 ,与
,与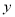 轴交于点
轴交于点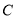 .
.(1)求二次函数的解析式,写出顶点坐标;
(2)动点
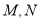 同时从
同时从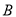 点出发,均以每秒2个单位长度的速度分别沿
点出发,均以每秒2个单位长度的速度分别沿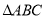 的
的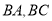 边上运动,设其运动的时间为
边上运动,设其运动的时间为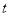 秒,当其中一个点到达终点时,另一个点也随之停止运动.连结
秒,当其中一个点到达终点时,另一个点也随之停止运动.连结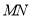 ,将
,将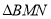 沿
沿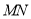 翻折,若点
翻折,若点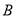 恰好落在抛物线弧上的
恰好落在抛物线弧上的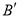 处,试求
处,试求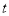 的值及点
的值及点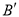 的坐标;
的坐标;(3)在(2)的条件下,Q为BN的中点,试探究坐标轴上是否存在点
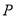 ,使得以
,使得以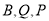 为顶点的三角形与
为顶点的三角形与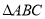 相似?如果存在,请求出点
相似?如果存在,请求出点 的坐标;如果不存在,试说明理由.
的坐标;如果不存在,试说明理由.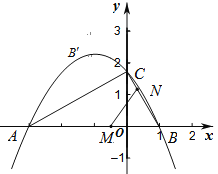
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a是b的近似值,那么我们把b叫做a的真值.若用四舍五入法得到的近似数是85,则下列各数不可能是其真值的是( )
A. 85.01 B. 84.51 C. 84.99 D. 84.49
相关试题

