【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(a,﹣a),点B坐标为(b,c),a,b,c满足 ![]() .
.
(1)若a没有平方根,判断点A在第几象限并说明理由;
(2)若点A到x轴的距离是点B到x轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,﹣2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
参考答案:
【答案】
(1)解:∵a没有平方根,
∴a<0,
∴﹣a>0,
∴点A在第二象限
(2)解:解方程组 ![]() ,用a表示b、c得b=a,c=4﹣a,
,用a表示b、c得b=a,c=4﹣a,
∴B点坐标为(a,4﹣a),
∵点A到x轴的距离是点B到x轴距离的3倍,
∴|﹣a|=3|4﹣a|,
当a=3(4﹣a),解得a=3,则c=4﹣3=1,此时B点坐标为(3,1);
当a=﹣3(4﹣a),解得a=6,则c=4﹣6=﹣2,此时B点坐标为(6,﹣2);
综上所述,B点坐标为(3,1)或(6,﹣2)
(3)解:∵点A的坐标为(a,﹣a),点B坐标为(a,4﹣a),
∴AB=4,AB与y轴平行,
∵点D的坐标为(4,﹣2),△OAB的面积是△DAB面积的2倍,
∴点A、点B在y轴的右侧,即a>0,
∴ ![]() ×4×a=2×
×4×a=2× ![]() ×4×|4﹣a|,解得a=
×4×|4﹣a|,解得a= ![]() 或a=8,
或a=8,
∴B点坐标为( ![]() ,
, ![]() )或(8,﹣4)
)或(8,﹣4)
【解析】(1)根据平方根的意义得到a<0,然后根据各象限点的坐标特征可判断点A在第二象限;(2)先利用方程组 ![]() ,用a表示b、c得b=a,c=4﹣a,则B点坐标为(a,4﹣a),再利用点A到x轴的距离是点B到x轴距离的3倍得到|﹣a|=3|4﹣a|,则a=3(4﹣a)或a=﹣3(4﹣a),分别解方程求出a的值,然后计算出c的值,于是可写出B点坐标;(3)利用A(a,﹣a)和B(a,4﹣a)得到AB=4,AB与y轴平行,由于点D的坐标为(4,﹣2),△OAB的面积是△DAB面积的2倍,则判断点A、点B在y轴的右侧,即a>0,根据三角形面积公式得到
,用a表示b、c得b=a,c=4﹣a,则B点坐标为(a,4﹣a),再利用点A到x轴的距离是点B到x轴距离的3倍得到|﹣a|=3|4﹣a|,则a=3(4﹣a)或a=﹣3(4﹣a),分别解方程求出a的值,然后计算出c的值,于是可写出B点坐标;(3)利用A(a,﹣a)和B(a,4﹣a)得到AB=4,AB与y轴平行,由于点D的坐标为(4,﹣2),△OAB的面积是△DAB面积的2倍,则判断点A、点B在y轴的右侧,即a>0,根据三角形面积公式得到 ![]() ×4×a=2×
×4×a=2× ![]() ×4×|4﹣a|,解方程得a=
×4×|4﹣a|,解方程得a= ![]() 或a=8,然后写出B点坐标.
或a=8,然后写出B点坐标.
【考点精析】掌握解三元一次方程组和三角形的面积是解答本题的根本,需要知道通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据专家估计,由山体滑坡形成的某堰塞湖的储水量约为2.12万m3,则关于“2.12万”下列说法正确的是( )
A. 精确到百分位 B. 精确到万位
C. 精确到千位 D. 精确到百位
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A组数据如下:0,1,-2,-1,0,-1,3
(1)求A组数据的平均数;
(2)从A组数据中选取5个数据,记这5个数据为B组数据,要求B组数据满足两个条件:①它的平均数与A组数据的平均数相等;②它的方差比A组数据的方差大.
请你选取B组的数据,并请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.

(1)求证:AB∥CD;
(2)H是直线CD上一动点(不与点D重合),BI平分∠HBD.写出∠EBI与∠BHD的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在Rt
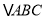 中,斜边
中,斜边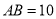 ,
, 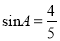 ,点P为边AB上一动点(不与A,B重合),PQ平分
,点P为边AB上一动点(不与A,B重合),PQ平分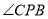 交边BC于点Q,
交边BC于点Q, 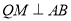 于
于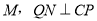 于N.
于N.(1)当AP=CP时,求
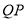 ;
;(2)若
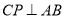 ,求CQ;
,求CQ;(3)探究:AP为何值时,四边形PMQN与
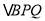 的面积相等?
的面积相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=3x+1的图象沿y轴向下平移2个单位长度,所得直线的函数表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
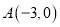 ,二次函数
,二次函数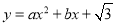 的对称轴为直线
的对称轴为直线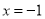 ,其图象过点
,其图象过点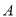 与
与 轴交于另一点
轴交于另一点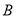 ,与
,与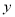 轴交于点
轴交于点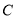 .
.(1)求二次函数的解析式,写出顶点坐标;
(2)动点
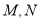 同时从
同时从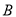 点出发,均以每秒2个单位长度的速度分别沿
点出发,均以每秒2个单位长度的速度分别沿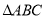 的
的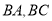 边上运动,设其运动的时间为
边上运动,设其运动的时间为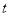 秒,当其中一个点到达终点时,另一个点也随之停止运动.连结
秒,当其中一个点到达终点时,另一个点也随之停止运动.连结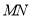 ,将
,将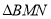 沿
沿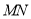 翻折,若点
翻折,若点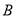 恰好落在抛物线弧上的
恰好落在抛物线弧上的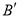 处,试求
处,试求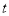 的值及点
的值及点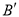 的坐标;
的坐标;(3)在(2)的条件下,Q为BN的中点,试探究坐标轴上是否存在点
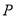 ,使得以
,使得以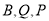 为顶点的三角形与
为顶点的三角形与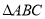 相似?如果存在,请求出点
相似?如果存在,请求出点 的坐标;如果不存在,试说明理由.
的坐标;如果不存在,试说明理由.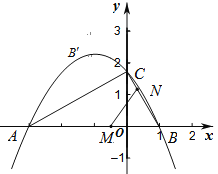
相关试题

