【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=![]() ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )

A. ②③B. ①②④C. ①③④D. ①②③④
参考答案:
【答案】B
【解析】
根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.
①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故正确;
②∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正确;
③条件不足,无法证明CA平分∠BCG,故错误;
④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+![]() (∠ABC+∠ACB)=135°,
(∠ABC+∠ACB)=135°,
∴∠DFE=360°-135°-90°=135°,
∴∠DFB=45°=![]() ∠CGE,,正确.
∠CGE,,正确.
故选B.
-
科目: 来源: 题型:
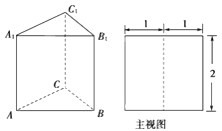
查看答案和解析>>【题目】如图,直三棱柱ABC-A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们把分一条线段为两条相等线段的点称为线段的中点.如图1所示,则称点M为线段AB的中点.
问题解决:
(1)如图2所示,点A、B、C、D、E在数轴上的对应的数分别为﹣2、﹣1、0、1、2,则图2中,线段AC的中点是点 ,点C是线段 和线段 的中点,线段AB的中点对应的数是 ,线段BE的中点对应的数是 ;
(2)如图3,点E、F对应的数分别是e、f,则线段EF的中点对应的数为 (用含e、f的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
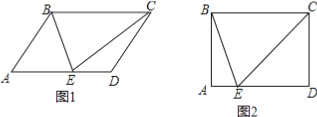
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
-
科目: 来源: 题型:
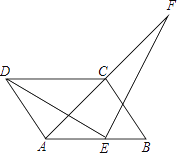
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)若ED=EF,ED与EF垂直吗?若垂直给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①△ABQ≌△CAP;;②∠CMQ的度数不变,始终等于60°③BP=CM;正确的有几个( )
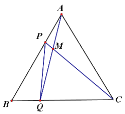
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
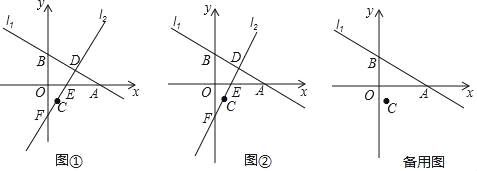
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线l1:y=k1x+2
 与x轴、y轴分别交于点A、B两点,OA=
与x轴、y轴分别交于点A、B两点,OA= OB,直线l2:y=k2x+b经过点C(1,﹣
OB,直线l2:y=k2x+b经过点C(1,﹣ ),与x轴、y轴和线段AB分别交于点E、F、D三点.
),与x轴、y轴和线段AB分别交于点E、F、D三点.(1)求直线l1的解析式;
(2)如图①:若EC=ED,求点D的坐标和△BFD的面积;
(3)如图②:在坐标轴上是否存在点P,使△PCD是以CD为底边的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
相关试题

