【题目】如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米? 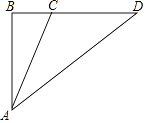
参考答案:
【答案】解:根据题意得:AC=CD,∠ABD=90°.
在直角三角形ABD中,
∵AB=3000,AD=5000,
∴BD= ![]() =4000(m),
=4000(m),
设CD=AC=x米,BC=4000﹣x(米),
在Rt△ABC中,AC2=AB2+BC2,
即x2=30002+(4000﹣x)2
解得:x=3125,
答:该超市与车站D的距离是3125米.
【解析】根据题意,AC=CD,∠ABD=90°,由AB、AD的长易求BD,设CD=x米,则AC=x,BC=BD﹣x.在直角三角形ABC中运用勾股定理得关系式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
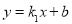 与反比例函数
与反比例函数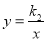 的图象交于第一象限内的
的图象交于第一象限内的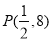 ,
,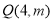 两点,与
两点,与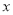 轴交于
轴交于 点.
点.
(1)分别求出这两个函数的表达式;
(2)写出点
 关于原点的对称点
关于原点的对称点 的坐标;
的坐标;(3)求
 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果向南走100米记作+100米,那么﹣10米表示的意义是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
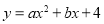 的图象与
的图象与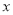 轴交于点
轴交于点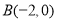 ,点
,点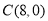 ,与
,与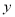 轴交于点
轴交于点 .
. 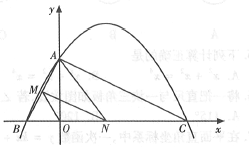
(1)求二次函数
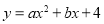 的表达式;
的表达式;(2)连接
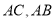 ,若点
,若点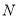 在线段
在线段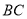 上运动(不与点
上运动(不与点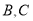 重合),过点
重合),过点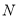 作
作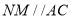 ,交
,交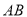 于点
于点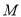 ,当
,当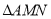 面积最大时,求N点的坐标;
面积最大时,求N点的坐标;(3)连接
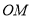 ,在(2)的结论下,求
,在(2)的结论下,求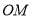 与
与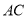 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.
x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.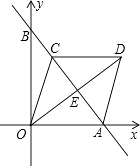
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=-2x+8中,若y>0,则( )
A. x<4 B. x>4 C. x>0 D. x<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
工种
人数
每人每月工资/元
电工
5
7000
木工
4
6000
瓦工
5
5000
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差(填“变小”、“不变”或“变大”).
相关试题

