【题目】如图,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.
x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.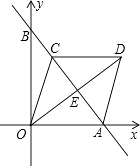
参考答案:
【答案】解:∵直线y=﹣ ![]() x+4与x轴、y轴分别交于点A,B,
x+4与x轴、y轴分别交于点A,B,
∴点A(3,0),点B(0,4),
∴OA=3,OB=4,
∴AB= ![]() =5.
=5.
∵四边形OADC是菱形,
∴OE⊥AB,OE=DE,
∴ ![]() OAOB=
OAOB= ![]() OEAB,即3×4=5OE,
OEAB,即3×4=5OE,
解得:OE= ![]() ,
,
∴OD=2OE= ![]() .
.
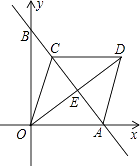
【解析】由直线AB的解析式利用一次函数图象上点的坐标特征可得出点A、B的坐标,进而可得出OA、OB的长度,由OA、OB的长度利用勾股定理可求出AB的长度,根据菱形的性质可得出OE⊥AB、OE=DE,利用面积相等法可求出OE的长度,再根据OD=2OE即可求出OD的长度.
【考点精析】根据题目的已知条件,利用一次函数的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果向南走100米记作+100米,那么﹣10米表示的意义是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
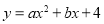 的图象与
的图象与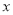 轴交于点
轴交于点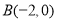 ,点
,点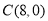 ,与
,与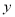 轴交于点
轴交于点 .
. 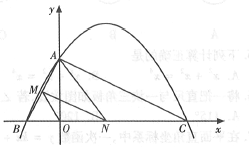
(1)求二次函数
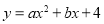 的表达式;
的表达式;(2)连接
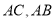 ,若点
,若点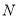 在线段
在线段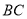 上运动(不与点
上运动(不与点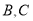 重合),过点
重合),过点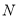 作
作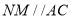 ,交
,交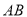 于点
于点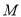 ,当
,当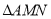 面积最大时,求N点的坐标;
面积最大时,求N点的坐标;(3)连接
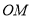 ,在(2)的结论下,求
,在(2)的结论下,求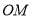 与
与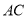 的数量关系.
的数量关系. -
科目: 来源: 题型:
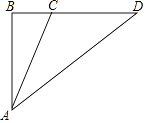
查看答案和解析>>【题目】如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=-2x+8中,若y>0,则( )
A. x<4 B. x>4 C. x>0 D. x<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
工种
人数
每人每月工资/元
电工
5
7000
木工
4
6000
瓦工
5
5000
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差(填“变小”、“不变”或“变大”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年10月16日上午7:45南京马拉松正式开跑,约21000名中外运动爱好者参加了此次活动.21000用科学记数法可表示为( )
A.0.21×105
B.0.21×104
C.2.1×104
D.2.1×103
相关试题

