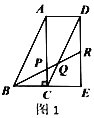
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
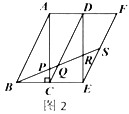
,易得![]() .若取四个直角三角形拼成如图2所示的形状,
.若取四个直角三角形拼成如图2所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
参考答案:
【答案】![]()
【解析】
首先证明△BCQ∽△BES,从而可求得CQ=![]() EF,DQ=
EF,DQ=![]() EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=![]() SE=
SE=![]() EF,
EF,
∴DQ=![]() EF,
EF,
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案为:4:1:3:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
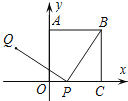
A.线段B.圆弧
C.双曲线的一部分D.抛物线的一部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3
 B. 2
B. 2 C. 5 D. 6
C. 5 D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系
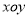 中,当
中,当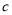 为何值时,抛物线
为何值时,抛物线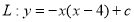 与直线段
与直线段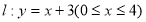 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:
有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:①当
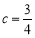 时,有唯一公共点;
时,有唯一公共点;②若
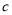 为整数,则仅当
为整数,则仅当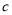 的值为4或5或6或7时,才有唯一公共点;
的值为4或5或6或7时,才有唯一公共点;③若
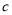 为整数,则当
为整数,则当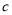 的值为1或2或3时,有两个公共点;
的值为1或2或3时,有两个公共点;④当
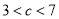 时,有两个公共点.其中正确的结论有( )
时,有两个公共点.其中正确的结论有( )A.①②④B.①②③C.①③D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=
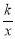 (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个函数给出如下定义:对于函数
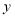 ,若当
,若当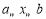 ,函数值
,函数值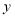 满足
满足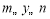 ,且满足
,且满足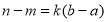 ,则称此函数为“
,则称此函数为“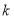 属和合函数”.
属和合函数”.例如:正比例函数
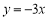 ,当
,当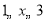 时,
时,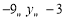 ,则
,则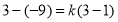 ,求得:
,求得: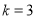 ,所以函数
,所以函数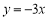 为“3属和合函数”.
为“3属和合函数”.(1)若一次函数
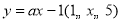 为“1属和合函数”,则
为“1属和合函数”,则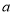 的值_________;
的值_________;(2)已知二次函数
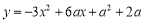 ,当
,当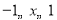 时,
时,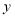 是“
是“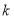 属和合函数”,则
属和合函数”,则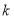 的取值范围_________.
的取值范围_________. -
科目: 来源: 题型:
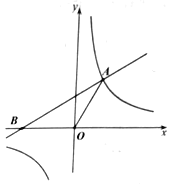
查看答案和解析>>【题目】已知:如图,一次函数
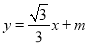 与反比例函数
与反比例函数 的图象在第一象限的交点为
的图象在第一象限的交点为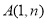 .
.
(1)求
 与
与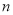 的值;
的值;(2)设一次函数的图像与
 轴交于点
轴交于点 ,连接
,连接 ,求
,求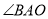 的度数.
的度数.
相关试题

