【题目】射线![]() 绕原点
绕原点![]() 从数轴的正半轴逆时针旋转一定的角度
从数轴的正半轴逆时针旋转一定的角度![]() (
(![]() ),射线上的一点
),射线上的一点![]() 与原点
与原点![]() 的距离(
的距离(![]() )为
)为![]() ,并规定:当
,并规定:当![]() 或
或![]() 时,点
时,点![]() 的位置记作
的位置记作![]() ;当
;当![]() 时,点
时,点![]() 的位置记作
的位置记作![]() .如图,点
.如图,点![]() 、
、![]() 的位置表示为
的位置表示为![]() ,
,![]() .回答下列问题:
.回答下列问题:
(1)已知点![]() ,点
,点![]() ,则点
,则点![]() 与点
与点![]() 的距离为 ;线段
的距离为 ;线段![]() 的中点
的中点![]() 的位置是( , ).
的位置是( , ).
(2)已知点![]() ,点
,点![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,以每秒2个单位长度的速度在线段
点出发,以每秒2个单位长度的速度在线段![]() 上来回运动;同时射线
上来回运动;同时射线![]() 以每秒10°的速度绕原点
以每秒10°的速度绕原点![]() 逆时针旋转,当时间
逆时针旋转,当时间![]() (其中
(其中![]() )为何值时,
)为何值时,![]() ?并求出此时三角形
?并求出此时三角形![]() 的面积.
的面积.
(3)直接写出位置满足![]() 的所有点所围成的图形面积.(结果保留一位小数)
的所有点所围成的图形面积.(结果保留一位小数)

参考答案:
【答案】(1)7;(250°,-0.5);(2)见解析;(3)39.3.
【解析】
(1)根据题意,画出图形进行计算即可得出答案;
(2)根据题意画出对应的图形,分两种情况讨论,再求其面积即可;
(3)满足![]() 的点在第一、四象限,以半径为5的半圆上的点,所围成的图形为半圆,计算半圆面积即可.
的点在第一、四象限,以半径为5的半圆上的点,所围成的图形为半圆,计算半圆面积即可.
解:(1)根据题意,画图得:
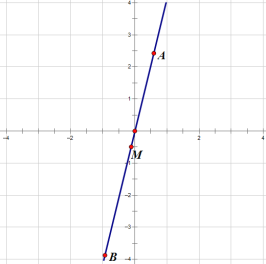
所以点A、B之间的距离为7,中点坐标为(250°,-0.5);
(2)如图所示:
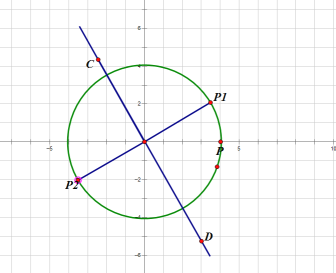
当![]() 逆时针旋转30°时,
逆时针旋转30°时,![]() .此时,
.此时, ![]() 秒
秒
点Q移动的长度为:![]()
∴OQ=1
∴![]()
当![]() 逆时针旋转210°时,
逆时针旋转210°时,![]() .此时,
.此时, ![]() 秒
秒
点Q移动的长度为:![]()
∴OQ=3
∴![]() .
.
(3)S=![]() .
.
-
科目: 来源: 题型:
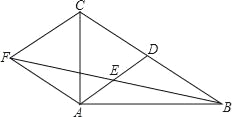
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)试判断四边形ADCF的形状,并证明;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m.
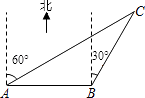
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列材料来自2006年5月衢州有关媒体的真实报道:有关部门进行民众安全感满意度调查,方法是:在全市内采用等距抽样,抽取32个小区,共960户,每户抽一名年满16周岁并能清楚表达意见的人,同时,对比前一年的调查结果,得到统计图如下:
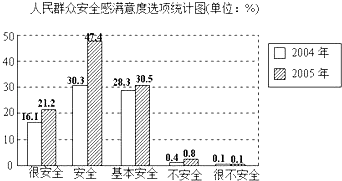
写出2005年民众安全感满意度的众数选项是;该统计图存在一个明显的错误是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】综合探究题 等腰三角形ABC中,AB=x,BC=y,周长为12.
(1)列出关于x,y的二元一次方程;
(2)求该方程的所有整数解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=
 ,反比例函数
,反比例函数  的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 
相关试题

