Question

【题目】如图，已知A、O、B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．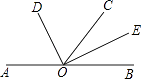

（1）若∠BOC=62°，求∠DOE的度数；
（2）若∠BOC=a°，求∠DOE的度数；
（3）图中是否有互余的角？若有请写出所有互余的角．

Answer 1

【答案】
（1）解：∵OD平分∠AOC，OE平分∠BOC，
∴∠DOC= ∠AOC，∠COE= ∠BOC
∴∠DOE=∠DOC+∠COE= （∠BOC+∠COA）= ×（62°+180°﹣62°）=90°
（2）解：∠DOE═ （∠BOC+∠COA）= ×（a°+180°﹣a°）=90°
（3）解：∠DOA与∠COE互余；∠DOA与∠BOE互余；∠DOC与∠COE互余；∠DOC与∠BOE互余 。
【解析】（1）根据角平分线的定义得出∠DOC= ∠AOC，∠COE= ∠BOC ，从而∠DOE=∠DOC+∠COE= （∠BOC+∠COA）= ×（62°+180°﹣62°）=90° ；
（2）根据角平分线的定义得出∠DOC= ∠AOC，∠COE= ∠BOC ，从而∠DOE=∠DOC+∠COE= （∠BOC+∠COA）= ×（α+180°﹣α）=90° ；
（3）根据互为余角的定义，只要相加等于90°的两个角就是互为余角，从而得出∠DOA与∠COE互余；∠DOA与∠BOE互余；∠DOC与∠COE互余；∠DOC与∠BOE互余
【考点精析】认真审题，首先需要了解角的平分线(从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线)，还要掌握余角和补角的特征(互余、互补是指两个角的数量关系，与两个角的位置无关)的相关知识才是答题的关键．