【题目】计算及解方程:
(1)化简:(5a2﹣ab)﹣2(3a2﹣ ![]() ab)
ab)
(2)解方程: ![]() ﹣
﹣ ![]() =1
=1
(3)先化简,再求值:3x2y﹣[2xy﹣2(xy﹣ ![]() x2y)+xy],其中x=3,y=﹣
x2y)+xy],其中x=3,y=﹣ ![]() .
.
参考答案:
【答案】
(1)解:原式=5a2﹣ab﹣6a2+ab=﹣a2
(2)解:去分母得:2(x﹣1)﹣(3x﹣1)=4,
去括号得:2x﹣2﹣3x+1=4,
移项合并得:﹣x=5,
解得:x=﹣5
(3)解:原式=3x2y﹣2xy+2xy﹣3x2y﹣xy=﹣xy,
当x=3,y=﹣ ![]() 时,原式=1
时,原式=1
【解析】(1)去括号,合并同类项,化为最简形式即可 ;
(2)去分母,去括号,移项合并同类项,系数化为1即可 ;
(3)先去小括号,再去中括号,然后合并同类项,再代入x,y的值计算即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=
 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
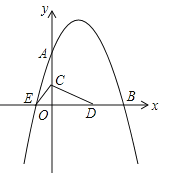
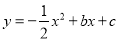 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,点P在∠AOB内部且OP=4,P1与P关于OB对称,P2与P关于OA对称,则P1P2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小河两岸边各有一棵树,分别高30尺和20尺,两树的距离是50尺,每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见水面上游出一条鱼,它们立刻飞去抓鱼,速度相同,并且同时到达目标.则这条鱼出现的地方离开比较高的树的距离为尺.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图表示一个点从数轴上的原点开始向右移动3个单位长度,再向左移动2个单位长度;这时表示什么数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
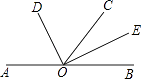
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
相关试题

