【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B、C重合).以AD为边做正方形ADEF,连接CF.
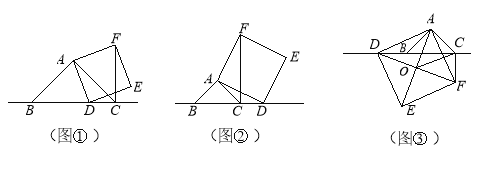
(1)如图①,当点D在线段BC上时,求证:CF+CD=BC;
(2)如图②,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其他条件不变;
①请直接写出CF、BC、CD三条线段之间的关系;
②若正方形ADEF的边长为![]() ,对角线AE、DF相交于点O,连接OC.求OC的长度.
,对角线AE、DF相交于点O,连接OC.求OC的长度.
参考答案:
【答案】(1)、证明过程见解析;(2)、CF-CD=BC;(3)、CD-CF=BC;2.
【解析】
试题分析:(1)、根据正方形的性质判定出△BAD和△CAF全等,从而得出BD=CF,根据BD+CD=BC得出答案;(2)、根据图形得出线段之间的关系;(3)、首先根据正方形的性质证明△BAD和△CAF全等,然后得出∠ACF=∠ABD=135°,从而说明△FCD为直角三角形,根据正方形的对角线得出DF的长度,然后根据直角三角形斜边上的中线的性质得出OC的长度.
试题解析:(1)、∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,∴∠BAD=∠CAF,
则在△BAD和△CAF中,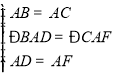 ∴△BAD ≌ △CAF(SAS),∴BD=CF,
∴△BAD ≌ △CAF(SAS),∴BD=CF,
∵BD+CD=BC,∴CF+CD=BC;
(2)、CF-CD=BC
(3)、①CD-CF =BC.
②∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF,
则在△BAD和△CAF中,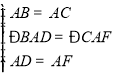 ∴△BAD ≌ △CAF(SAS),
∴△BAD ≌ △CAF(SAS),
∴∠ABD=∠ACF,∵∠ABC=45°,∠ABD=135°, ∴∠ACF=∠ABD=135°,
∴∠FCD=90°,∴△FCD是直角三角形. ∵正方形ADEF的边长为![]() 且对角线AE、DF相交于点O,
且对角线AE、DF相交于点O,
∴DF=![]() AD=4,O为DF中点. ∴OC=
AD=4,O为DF中点. ∴OC=![]() DF=2.
DF=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣8y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x﹣1)※x的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个一元一次方程,使得这个方程的解为“x=1”:_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据规定:距离高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°,AD=220.某人看中了①号楼A单元的一套住宅,但是感觉小区距离高铁轨道这么近,易受噪音污染,而售楼人员却说,虽然A单元离高铁轨道最近,但是AD长达220米,是达到设计要求的.
(1) 你认为售楼人员的话是否可信?为什么?
(2) 若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?(参考数据:
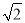 ≈1.4,
≈1.4, 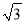 ≈1.7,
≈1.7, 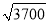 ≈61)
≈61)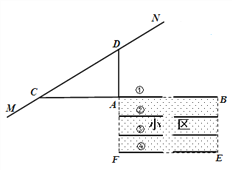
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,则这组数据的中位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在第四象限,且到x轴的距离是3,到y轴的距离是2,则点P的坐标为 .
相关试题

