【题目】如图，在平面直角坐标系xOy中，一次函数y=﹣2x的图象与反比例函数y= 的图象交于点A（﹣1，n）．

（1）求反比例函数y= 的解析式；
（2）若P是坐标轴上一点，且满足PA=OA，直接写出点P的坐标．

参考答案：

【答案】
（1）解：把A（﹣1，n）代入y=﹣2x得n=﹣2×（﹣1）=2，

∴A点坐标为（﹣1，2），

把A（﹣1，2）代入y= 得k=﹣1×2=﹣2，

∴反比例函数的解析式为y=﹣


（2）解：过A作AB⊥x轴于点B，AC⊥y轴于点C，如图，

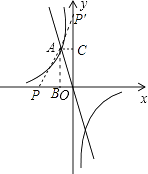
∵点A的坐标为（﹣1，2），

∴B点坐标为（﹣1，0），C点坐标为（0，2）

∴当P在x轴上，其坐标为（﹣2，0）；

当P点在y轴上，其坐标为（0，4）；

∴点P的坐标为（﹣2，0）或（0，4）．


【解析】（1）把点A的坐标代入一次函数y=﹣2x得解析式可求出点A的坐标，再把点A的坐标代入反比例函数y=可求出答案；
（2）过A作AB⊥x轴于点B，AC⊥y轴于点C，可得B点坐标、C点坐标，然后分P点在x轴上和在y轴上求出其坐标.

关闭