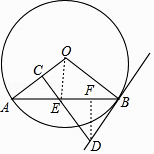
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵AO=OB,
∴∠OAB=∠OBA,
∵BD是切线,
∴OB⊥BD,
∴∠OBD=90°,
∴∠OBE+∠EBD=90°,
∵EC⊥OA,
∴∠CAE+∠CEA=90°,
∵∠CEA=∠DEB,
∴∠EBD=∠BED,
∴DB=DE
(2)作DF⊥AB于F,连接OE.
∵DB=DE,AE=EB=6,
∴EF= ![]() BE=3,OE⊥AB,
BE=3,OE⊥AB,
在Rt△EDF中,DE=BD=5,EF=3,
∴DF= ![]() =4,
=4,
∵∠AOE+∠A=90°,∠DEF+∠A=90°,
∴∠AOE=∠DEF,
∴sin∠DEF=sin∠AOE= ![]() =
= ![]() ,
,
∵AE=6,
∴AO= ![]() .
.
∴⊙O的半径为 ![]() .
.
【解析】(1)欲证明DB=DE,只要证明∠DEB=∠DBE;(2)作DF⊥AB于F,连接OE.只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE= ![]() =
= ![]() ,由此求出AE即可解决问题.
,由此求出AE即可解决问题.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与坐标轴分别交于
与坐标轴分别交于 ,
, 两点,以线段
两点,以线段 为边,在第一象限内作正方形
为边,在第一象限内作正方形 ,将正方形
,将正方形 沿
沿 轴负方向,平移
轴负方向,平移 个单位长度,使点
个单位长度,使点 恰好落在直线
恰好落在直线 上,则
上,则 的值为________.
的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
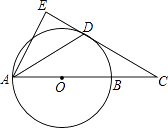
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3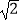 ,求弦AD的长.
,求弦AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.

(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系
 中,点
中,点 是直线
是直线 上一动点,将点
上一动点,将点 向右平移1个单位得到点
向右平移1个单位得到点 ,点
,点 ,则
,则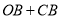 的最小值为________.
的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,
 =
= 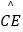

(1)求证:OA=OB;
(2)已知AB=4 ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.
相关试题

