【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, ![]() =
= ![]()

(1)求证:OA=OB;
(2)已知AB=4 ![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.
参考答案:
【答案】
(1)解:连接OC,
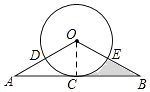
∵AB与⊙O相切于点C
∴∠ACO=90°,
由于 ![]() =
= ![]() ,
,
∴∠AOC=∠BOC,
∴∠A=∠B
∴OA=OB,
(2)解:由(1)可知:△OAB是等腰三角形,
∴BC= ![]() AB=2
AB=2 ![]() ,
,
∴sin∠COB= ![]() =
= ![]() ,
,
∴∠COB=60°,
∴∠B=30°,
∴OC= ![]() OB=2,
OB=2,
∴扇形OCE的面积为: ![]() =
= ![]() ,
,
△OCB的面积为: ![]() ×2
×2 ![]() ×2=2
×2=2 ![]()
∴S阴影=2 ![]() ﹣
﹣ ![]() π
π
【解析】(1)连接OC,由切线的性质可知∠ACO=90°,由于 ![]() =
= ![]() ,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;(2)由(1)可知:△AOB是等腰三角形,所以AC=2
,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;(2)由(1)可知:△AOB是等腰三角形,所以AC=2 ![]() ,从可求出扇形OCE的面积以及△OCB的面积
,从可求出扇形OCE的面积以及△OCB的面积
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.

(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系
 中,点
中,点 是直线
是直线 上一动点,将点
上一动点,将点 向右平移1个单位得到点
向右平移1个单位得到点 ,点
,点 ,则
,则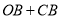 的最小值为________.
的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵
 两次共花费940元
两次共花费940元 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同 .
. 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元? 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵 、B两种花草价格不变
、B两种花草价格不变 ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量
 (吨)
(吨)频数
频率

6
0.12

________
0.24

16
0.32

10
0.20
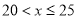
4
________

2
0.04

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
相关试题

