【题目】平面内有三点A(2,2 ![]() ),B(5,2
),B(5,2 ![]() ),C(5,
),C(5, ![]() ).
).
(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐标.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移3 ![]() 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标.
参考答案:
【答案】
(1)解:由题意知,四边形ABCD是矩形,
∴AB∥DC,
又∵AB平行于x轴(由AB两点的坐标可知),
∴DC也平行于x轴(平行线的性质),
∵AB⊥AD,
∴AD垂直于x轴.
∴D点既在经过C(5, ![]() )平行于x轴的平行线DC上,又在经过A(2,2
)平行于x轴的平行线DC上,又在经过A(2,2 ![]() )的x轴的垂线AD上,
)的x轴的垂线AD上,
∴D(2, ![]() )
)
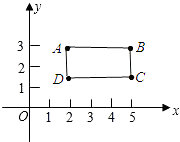
(2)解:由题意可知:AB=5﹣2=3,
AD=2 ![]() ,
,
故四边形ABCD的面积是AB×AD=3 ![]()
(3)解:∵四边形ABCD向右平移2个单位,再向下平移3 ![]() 个单位,
个单位,
∴A(2+2,2 ![]() ﹣3
﹣3 ![]() ),B(5+2,2
),B(5+2,2 ![]() ﹣3
﹣3 ![]() ),C(5+2,
),C(5+2, ![]() ﹣3
﹣3 ![]() ),D(2+2,
),D(2+2, ![]() ﹣3
﹣3 ![]() ),
),
即A(4,﹣ ![]() ),B(7,﹣
),B(7,﹣ ![]() ),C(7,﹣2
),C(7,﹣2 ![]() ),D(4,﹣2
),D(4,﹣2 ![]() ).
).
【解析】(1)抓住矩形的特点,即对边平行,邻边互相垂直的性质,AB∥DC,AB⊥DC,BC∥AD,BC⊥AD及平行线的性质,第三条直线与平行线中的任何一条平行,那么,它与另一条也平行.(2)根据两点间的距离公式求出边长,再根据矩形的面积公式求出面积.(3)根据平移及点的移动规律即可得解.
【考点精析】利用三角形的面积和坐标与图形变化-平移对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题9分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
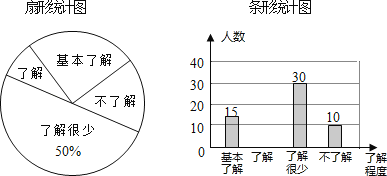
(1)接受问卷调查的学生共有___名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式4x2y﹣5x3y2+7xy3﹣6的次数是( )
A.4
B.5
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x-2)(x-1)=x2-3x+2,则x2-3x+2因式分解的结果为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣2x-m=0有两个不相同的实数根,则实数m的取值范围是( )
A. m≥-1B. m≤1C. m>-1D. m<-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABC和∠ACB的平分线交于点O,EF经过点O且平行于BC,分别与AB,AC交于点E,F.
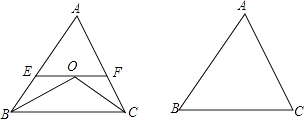
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠ABC=α,∠ACB=β,用α,β的代数式表示∠BOC的度数.
(3)在第(2)问的条件下,若∠ABC和∠ACB邻补角的平分线交于点O,其他条件不变,请画出相应图形,并用α,β的代数式表示∠BOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】“我们可以在同一条数轴上表示两个不等式的解集,观察数轴,找出它们解集的公共部分,从而得到不等式组的解集”在这种解不等式组的方法中所体现出来的数学思想是( )
A. 消元 B. 换元 C. 数形结合 D. 分类讨论
相关试题

