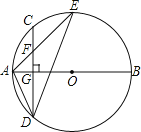
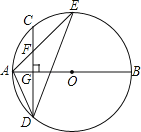
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.
参考答案:
【答案】①证明见解析;
②2;
③证明见解析.
【解析】试题分析:(1)由垂径定理可得弧AC=弧AD,根据等弧所对的圆周角相等,可得∠ADF=∠AED,,根据两角对应相等的两个三角形相似的判定定理,即可证得△ADF∽△AED;
(2)根据![]() =
=![]() ,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
(3)在Rt△AGF中由勾股定理求得AG的长,根据垂径定理和同弧所对的圆周角相等的性质,可知∠E=∠ADF,再根据三角函数定义即可证得tanE的值.
解:①∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
②∵![]() =
=![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
③∵AF=3,FG=2,∴AG=![]() ,
,
tan∠E=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并回答下列问题:
小明遇到这样一个问题,如图,在
 中,
中, 分别交
分别交 于点
于点 ,交
,交 于点
于点 .已知
.已知 ,求
,求 的值.
的值.小明发现,过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,构造
,构造 ,经过推理和计算能够使问题得到解决(如图)
,经过推理和计算能够使问题得到解决(如图)
请你回答:
(1)证明:
 ;
;(2)求出
 的值;
的值;(3)参考小明思考问题的方法,解决问题;
如图,已知
 和矩形
和矩形 与
与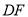 交于点
交于点 .求
.求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中错误的是_______.
A. 有一个角是
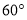 的等腰三角形是等边三角形;
的等腰三角形是等边三角形;B. 连接等边三角形三边中点所构成的三角形,也是等边三角形:
C. 三角形的外角和为
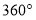
D. 等腰三角形的对称轴是顶角平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于
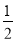 MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=
MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=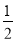 ∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
∠ABC;③BC=BE;④AE=BE中,一定正确的是( )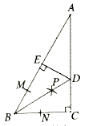
A. ①②③B. ① ② ④C. ①③④D. ②③④
-
科目: 来源: 题型:
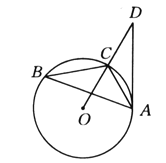
查看答案和解析>>【题目】如图所示,已知△ABC内接于⊙O,点D在OC的延长线上,sin B=
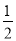 ,∠D=30°.
,∠D=30°.(1)求证AD是⊙O的切线;
(2)若AC=6,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦BC=9,∠BOC=50°,OE⊥AC,垂足为E.

(1)求OE的长.
(2)求劣弧AC的长(结果精确到0.1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
 ,
, ,
, ,且
,且 、
、 、
、 三点在一直线上,请填写
三点在一直线上,请填写 的理由.
的理由.
解:在
 与
与 中,
中, (已知),
(已知), (已知),
(已知), (已知),
(已知),所以

所以

 ________(________)
________(________)所以
 (等式性质),
(等式性质),即
 ________
________ ________.
________.因为
 (________)
(________)即
 ,
,所以
 (________).
(________).所以
 (等量代换).
(等量代换).
相关试题

