搜索
【题目】如图，AB是⊙O的直径，弦BC=9，∠BOC=50°，OE⊥AC，垂足为E．
（1）求OE的长．
（2）求劣弧AC的长(结果精确到0．1)．
参考答案：
【答案】（1）4.5（2）24.2
【解析】（1）∵OE⊥AC，OE为直径的一部分
∴AE=EC （2分）
又∵AO=BO
∴
（2分）
（2）∵∠COB=50°
∴∠AOC=130° （1分）
∵AO=CO，OE⊥AC
∴∠AOE=
∠AOC =65°（2分）
∴
∴AO=
（1分）
∴
（2分）
（1）由垂径定理知，由E是AC的中点，点O是AB的中点，则OB是△ABC的BC边对的中位线，所以OE=BC÷2；
（2）由圆周角定理得，∠A=∠BDC=25°，由等边对等角得∠OCA=∠A，由三角形内角和定理求得∠AOC的度数，再利用弧长公式求得弧AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于
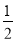MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED；②∠ABD=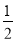∠ABC；③BC=BE；④AE=BE中，一定正确的是（ ）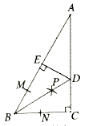
A. ①②③B. ① ② ④C. ①③④D. ②③④
-
科目： 来源： 题型：
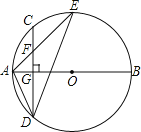
查看答案和解析>>【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足
=
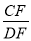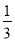，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．（1）求证：△ADF∽△AED；
（2）求FG的长；
（3）求证：tan∠E=
．
-
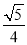科目： 来源： 题型：
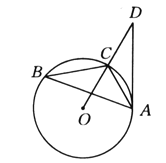
查看答案和解析>>【题目】如图所示，已知△ABC内接于⊙O，点D在OC的延长线上，sin B＝
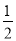，∠D＝30°．(1)求证AD是⊙O的切线；
(2)若AC＝6，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：
，
，
，且
、
、
三点在一直线上，请填写
的理由.
解：在
与
中，（已知），（已知），（已知），所以
所以
________（________）所以
（等式性质），即
________
________.因为
（________）即
，所以
（________）.所以
（等量代换）. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，为一幅重叠放置的三角板，其中∠ABC=∠EDF=90°，BC与DF共线，将△DEF沿CB方向平移，当EF经过AC的中点O时，直线EF交AB于点G，若BC=3，则此时OG的长度为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图 (1)所示，圆内接△ABC中，AB＝BC＝CA，OD，OE为⊙O的半径，OD⊥BC于点F，OE⊥AC于点G．
(1)求证阴影部分四边形OFCG的面积是△ABC面积的
；(2)如图 (2)所示，若∠DOE保持120°角度不变，求证当∠DOE绕着O点旋转时，由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的
．
相关试题
