【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
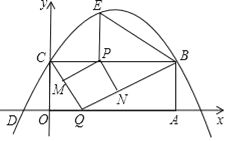
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
参考答案:
【答案】(1)![]() ;(2)t=3;(3)
;(2)t=3;(3)![]() 或
或![]()
【解析】试题分析:(1)由抛物线的解析式可求得C点坐标,由矩形的性质可求得B点坐标,由B、D的坐标,利用待定系数法可求得抛物线解析式;
(2)可设P(t,4),则可表示出E点坐标,从而可表示出PB、PE的长,由条件可证得△PBE∽△OCD,利用相似三角形的性质可得到关于t的方程,可求得t的值;
(3)当四边形PMQN为正方形时,则可证得△COQ∽△QAB,利用相似三角形的性质可求得CQ的长,在Rt△BCQ中可求得BQ、CQ,则可用t分别表示出PM和PN,可得到关于t的方程,可求得t的值.
试题解析:
解:(1)在y=ax2+bx+4中,令x=0可得y=4,
∴C(0,4),
∵四边形OABC为矩形,且A(10,0),
∴B(10,4),
把B、D坐标代入抛物线解析式可得![]() ,
,
解得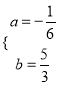 ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+4;
x+4;
(2)由题意可设P(t,4),则E(t, ![]() t2+
t2+![]() t+4),
t+4),
∴PB=10﹣t,PE=![]() t2+
t2+![]() t+4﹣4=
t+4﹣4=![]() t2+
t2+![]() t,
t,
∵∠BPE=∠COD=90°,
当∠PBE=∠OCD时,
则△PBE∽△OCD,
∴![]() ,即BPOD=COPE,
,即BPOD=COPE,
∴2(10﹣t)=4(![]() t2+
t2+![]() t),解得t=3或t=10
t),解得t=3或t=10
∴当t=3时,∠PBE=∠OCD;
当∠PBE=∠CDO时,
则△PBE∽△ODC,
∴![]() ,即BPOC=DOPE,
,即BPOC=DOPE,
∴4(10﹣t)=2(![]() t2+
t2+![]() t),解得t=12或t=10(均不合题意,舍去)
t),解得t=12或t=10(均不合题意,舍去)
综上所述∴当t=3时,∠PBE=∠OCD;
(3)当四边形PMQN为正方形时,则∠PMC=∠PNB=∠CQB=90°,PM=PN,
∴∠CQO+∠AQB=90°,
∵∠CQO+∠OCQ=90°,
∴∠OCQ=∠AQB,
∴Rt△COQ∽Rt△QAB,
∴![]() ,即OQAQ=COAB,
,即OQAQ=COAB,
设OQ=m,则AQ=10﹣m,
∴m(10﹣m)=4×4,解得m=2或m=8,
①当m=2时,CQ=![]() =
=![]() ,BQ=
,BQ=![]() =
=![]() ,
,
∴sin∠BCQ=![]() =
=![]() ,sin∠CBQ=
,sin∠CBQ=![]() =
=![]() ,
,
∴PM=PCsin∠PCQ=![]() t,PN=PBsin∠CBQ=
t,PN=PBsin∠CBQ=![]() (10﹣t),
(10﹣t),
∴![]() t =
t =![]() (10﹣t),解得t=
(10﹣t),解得t=![]() ,
,
②当m=8时,同理可求得t=![]() ,
,
∴当四边形PMQN为正方形时,t的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=-x2+2x+3与x轴相交于A.B两点(点A在B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF//DE交抛物线于点F,设点P的横坐标为m:
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
-
科目: 来源: 题型:
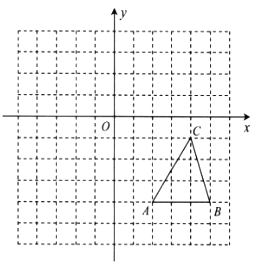
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系,已知
 的顶点
的顶点 的坐标为
的坐标为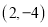 ,顶点
,顶点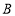 的坐标为
的坐标为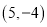 ,顶点
,顶点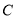 的坐标为
的坐标为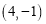 .
.
(1)求
 的面积;
的面积;(2)若把
 向上平移3个单位长度,再向左平移6个单位长度得到
向上平移3个单位长度,再向左平移6个单位长度得到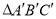 ,请画出
,请画出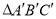 ;
;(3)若点
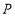 在
在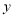 轴上,且
轴上,且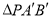 的面积与
的面积与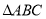 的面积相等,请直接写出点
的面积相等,请直接写出点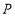 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置的
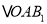 ,
,  ,
, 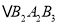 ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边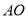 在
在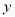 轴上,点
轴上,点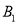 ,
, 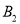 ,
, 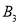 ,…都在直线
,…都在直线 上,则
上,则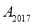 的坐标是( )
的坐标是( )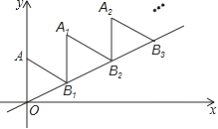
A. (2017,2017
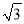 ) B. (2017
) B. (2017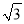 ,2017)
,2017)C. (2017,2018) D. (2017
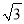 ,2019)
,2019) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:
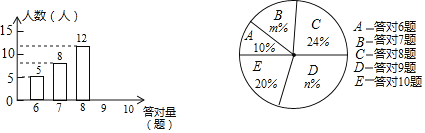
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
相关试题

