【题目】抛物线y=-x2+2x+3与x轴相交于A.B两点(点A在B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF//DE交抛物线于点F,设点P的横坐标为m:
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
参考答案:
【答案】(1)A(-1,0),B(3,0),C(0,3);抛物线的对称轴是:x=1.(2)①当m=2时,四边形PEDF为平行四边形;②![]() .
.
【解析】试题分析: (1)对于抛物线解析式,令y=0求出![]() 的值,确定出A与B坐标,令x=0求出
的值,确定出A与B坐标,令x=0求出![]() 的值确定出
的值确定出![]() 坐标,进而求出对称轴即可;
坐标,进而求出对称轴即可;
(2)①根据![]() 与
与![]() 坐标,利用待定系数法确定出直线
坐标,利用待定系数法确定出直线![]() 解析式,进而表示出
解析式,进而表示出![]() 与
与![]() 坐标,根据抛物线解析式确定出
坐标,根据抛物线解析式确定出![]() 与
与![]() 坐标,表示出
坐标,表示出![]() ,利用平行四边形的判定方法确定出
,利用平行四边形的判定方法确定出![]() 的值即可;
的值即可;
②连接![]() ,设直线
,设直线![]() 与x轴交于点M,,求出
与x轴交于点M,,求出![]() 的长,根据
的长,根据![]() ,列出
,列出![]() 关于
关于![]() 的二次函数解析式.
的二次函数解析式.
试题解析:(1)对于抛物线![]()
令x=0,得到y=3;
令y=0,得到![]() ,即(x3)(x+1)=0,
,即(x3)(x+1)=0,
解得:x=1或x=3,
则A(1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
(2)①设直线BC的函数解析式为y=kx+b,
把B(3,0),C(0,3)分别代入得:![]()
解得:k=1,b3,
∴直线BC的解析式为y=x+3,
当x=1时,y=1+3=2,
∴E(1,2),
当x=m时,y=m+3,
∴P(m,m+3),
令![]() 中x=1,得到y=4,
中x=1,得到y=4,
∴D(1,4),
当x=m时,![]()
![]()
∴线段DE=42=2,
∵0<m<3,
![]()
∴线段![]()
连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,
由![]() 得到m=2或m=1(不合题意,舍去),
得到m=2或m=1(不合题意,舍去),
则当m=2时,四边形PEDF为平行四边形;
②连接BF,设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3,
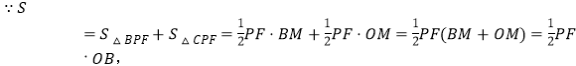
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定搞错了.”
(1)王老师为什么说他搞错了?试用方程的知识给予解释;
(2)陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本.但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,笔记本的单价可能为多少元?
-
科目: 来源: 题型:
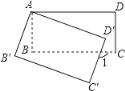
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°).若∠1=115°,则∠α=____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=
 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).

图1 图2 图3
-
科目: 来源: 题型:
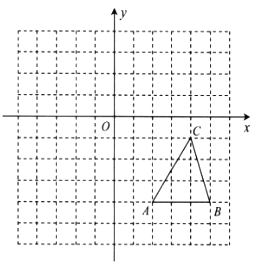
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系,已知
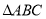 的顶点
的顶点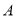 的坐标为
的坐标为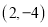 ,顶点
,顶点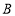 的坐标为
的坐标为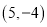 ,顶点
,顶点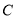 的坐标为
的坐标为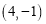 .
.
(1)求
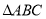 的面积;
的面积;(2)若把
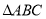 向上平移3个单位长度,再向左平移6个单位长度得到
向上平移3个单位长度,再向左平移6个单位长度得到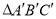 ,请画出
,请画出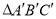 ;
;(3)若点
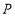 在
在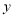 轴上,且
轴上,且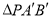 的面积与
的面积与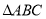 的面积相等,请直接写出点
的面积相等,请直接写出点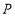 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置的
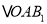 ,
,  ,
, 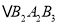 ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边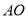 在
在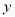 轴上,点
轴上,点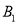 ,
, 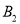 ,
, 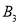 ,…都在直线
,…都在直线 上,则
上,则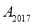 的坐标是( )
的坐标是( )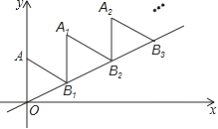
A. (2017,2017
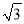 ) B. (2017
) B. (2017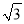 ,2017)
,2017)C. (2017,2018) D. (2017
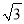 ,2019)
,2019) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
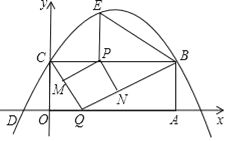
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
相关试题

