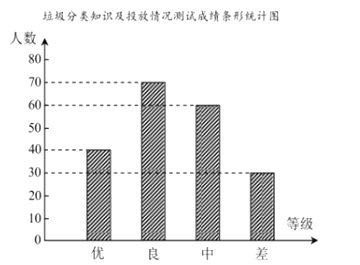
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
参考答案:
【答案】(1)![]() ;(2)200人;(3)60人;(4)1650人
;(2)200人;(3)60人;(4)1650人
【解析】
(1)用成绩是“优”所在扇形圆心角的度数除以360°即可;
(2)用成绩是“优”的人数除以所占的百分比即可;
(3)利用总人数减去其它组的人数即可求得成绩是“中”的人数,从而补全条形图;
(4)利用总人数3000乘以成绩是“优”和“良”的学生所占的百分比即可.
解:(1)成绩是“优秀”的人数占抽取人数的百分比是![]() .
.
(2)本次随机抽取问卷测试的人数是![]() 人.
人.
(3)成绩是“中”的人数为![]() 人.
人.
补充的条形统计图如图所示:
(4)估计成绩是“优”和“良”的学生共约有![]() 人.
人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
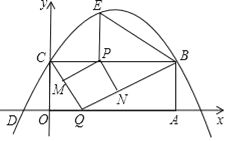
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:
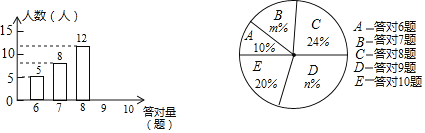
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD 与正方形
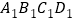 关于某点中心对称.已知A,
关于某点中心对称.已知A,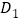 ,D三点的坐标分别是(0,4),(0,3),(0,2).
,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标:
(2)写出顶点B,C,
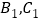 的坐标。
的坐标。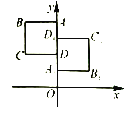
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年农历五月初五,是中国民间的传统节日——端午节.它始于我国的春秋战国时期,已列为世界非物质文化遗产.时至今日,端午节在我国仍是一个十分盛行的节日.今年端午节,某地甲、乙两家超市为吸引更多的顾客,开展促销活动,对某种质量和售价相同的粽子分别推出了不同的优惠方案.甲超市的方案是:购买该种粽子超过80元后,超出80元的部分按九折收费;乙超市的方案是:购买该种粽子超过120元后,超出120元的部分按八折收费.请根据顾客购买粽子的金额,选择到哪家超市购买粽子划算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】东营市某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
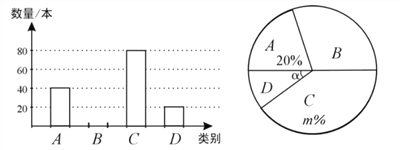
(1)这次统计共抽取_____本书籍,扇形统计图中的m=______,∠α的度数是_____
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
相关试题

