【题目】如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系,已知![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
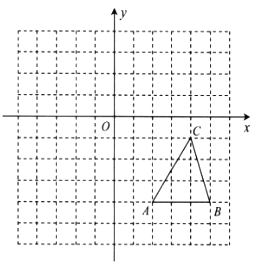
(1)求![]() 的面积;
的面积;
(2)若把![]() 向上平移3个单位长度,再向左平移6个单位长度得到
向上平移3个单位长度,再向左平移6个单位长度得到![]() ,请画出
,请画出![]() ;
;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积与
的面积与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)点
;(2)见解析;(3)点![]() 的坐标是
的坐标是![]() 或
或![]()
【解析】
(1)利用三角形面积公式计算;
(2)利用点平移的坐标变换规律写出A′、B′、C′的坐标,然后描点即可;
(3)设P(0,t),根据三角形面积公式得到![]() ×3×|t+1|=
×3×|t+1|=![]() ,然后求出t即可得到P点坐标.
,然后求出t即可得到P点坐标.
解:(1)![]() 的面积等于
的面积等于![]() .
.
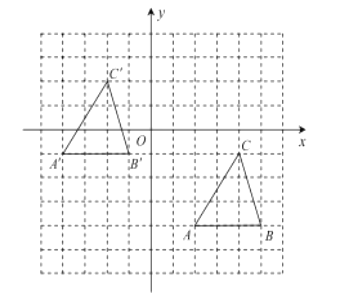
(2)画出的![]() 如图所示:
如图所示:
(3)设P(0,t),
∵△PA′B′的面积与△ABC的面积相等,
∴![]() ×3×|t+1|=
×3×|t+1|=![]() ,解得t=2或t=-4,
,解得t=2或t=-4,
∴P点坐标为(0,2)或(0,-4).
-
科目: 来源: 题型:
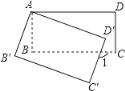
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°).若∠1=115°,则∠α=____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=
 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).

图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=-x2+2x+3与x轴相交于A.B两点(点A在B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF//DE交抛物线于点F,设点P的横坐标为m:
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置的
 ,
,  ,
, 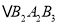 ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边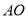 在
在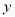 轴上,点
轴上,点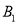 ,
, 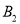 ,
, 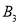 ,…都在直线
,…都在直线 上,则
上,则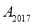 的坐标是( )
的坐标是( )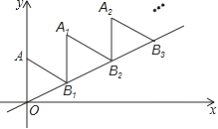
A. (2017,2017
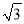 ) B. (2017
) B. (2017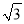 ,2017)
,2017)C. (2017,2018) D. (2017
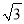 ,2019)
,2019) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
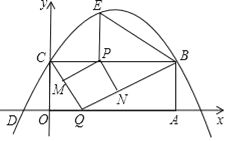
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:
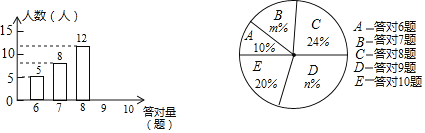
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
相关试题

