【题目】如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.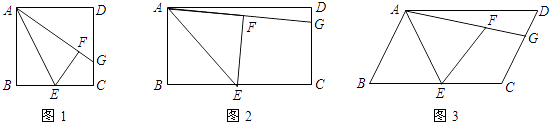
(1)猜想并证明线段GF与GC的数量关系;
(2)若将图1中的正方形改成矩形,其它条件不变,如图2,那么线段GF与GC之间的数量关系是否改变?请证明你的结论;
(3)若将图1中的正方形改成平行四边形,其它条件不变,如图3,那么线段GF与GC之间的数量关系是否会改变?请证明你的结论.
参考答案:
【答案】
(1)
解:FG=CG,理由如下:
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,
∴EF=EC;
同样,在折叠中,∠B=∠EFA=90°
又∵∠C=∠B,∠EFG=∠EFA
∴∠C=∠EFG=90°
∵EG=EG,
∴△ECG≌△EFG
∴FG=CG
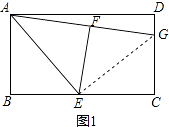
(2)
解:不会改变.
证明:连接EG
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,
∴EF=EC;
同样,在折叠中,∠B=∠EFA=90°
又∵∠C=∠B,∠EFG=∠EFA
∴∠C=∠EFG=90°
∵EG=EG,
∴△ECG≌△EFG
∴FG=CG;
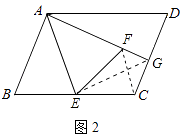
(3)
解:不会改变.
证明:连接EG、FC
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,∠B=∠AFE
∴EF=EC
∴∠EFC=∠ECF
∵矩形ABCD改为平行四边形
∴∠B=∠D
∵∠ECD=180°﹣∠D,∠EFG=180°﹣∠AFE=180°﹣∠B=180°﹣∠D
∴∠ECD=∠EFG
∴∠GFC=∠GFE﹣∠EFC=∠ECG﹣∠ECF=∠GCF
∴∠GFC=∠GCF
∴△ECG≌△EFG
∴FG=CG
即(1)中的结论仍然成立
【解析】(1)判定直角三角形△ECG和△EFG全等,和全等三角形对应边相等的性质;(2)判定直角三角形△ECG和△EFG全等,和全等三角形对应边相等的性质;(3)判定△ECG和△EFG全等,根据全等三角形对应边相等性质即可证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店老板以每斤x元的单价购进草莓100斤,加价30%卖出70斤以后,每斤比进价降低a元,将剩下30斤全部卖出,则可获得利润为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不论x为何值,等式x(2x+a)+4x﹣3b=2x2+5x+b恒成立,则a,b的值应分别是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣3x﹣4=0根的判别式的值等于_____.
-
科目: 来源: 题型:
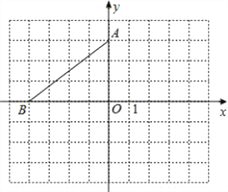
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)请在图中画出△AEF.
(2)请在x轴上找一个点P,使PA+PE的值最小,并直接写出P点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题
①两条对角线互相平分的四边形是平行四边形;
②两条对角线相等的四边形是矩形;
③两条对角线互相垂直的平行四边形是菱形;
④有一组邻边相等且有一个角是直角的四边形是正方形,
其中是真命题的是( )
A.①②B.③④C.①③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将直线y=﹣2x向上平移3个单位后得到直线AB,那么直线AB的解析式是_____.
相关试题

