【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.
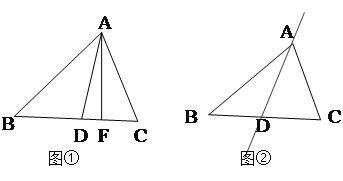
(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
参考答案:
【答案】(1)∠DAF=5°(2)∠DEF=![]() (β-α)
(β-α)
【解析】试题分析:根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由垂直的定义可得∠AFC的度数,根据直角三角形的两锐角互余即可求得∠DAF的度数;(2)如图2,根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由三角形的内角和定理求得∠ADC的度数,再由垂直的定义可得∠EFD的度数,根据直角三角形的两锐角互余即可求得∠DEF的度数;如图3,类比图2的方法解决问题即可.
试题解析:
(1)∵∠B=500,∠C=600,
∴∠BAC=180°-∠B-∠C=180°-500-600 =70°,
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() ×70°=35°,
×70°=35°,
又∵AF⊥BC ,
∴∠AFC =90°,
∴∠CAF =90° -∠C =30°,
∴ ∠DAF =∠CAD -∠CAF =5°.
(2)① 如图,

图2
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠ADC =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).
②如图,
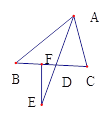
图3
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
∴∠ADC=∠EDF=90°+![]() α-
α-![]() β,
β,
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠EDF =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).
-
科目: 来源: 题型:
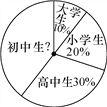
查看答案和解析>>【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人
捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均 每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2、3中的a= , b=;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
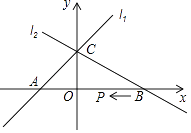
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
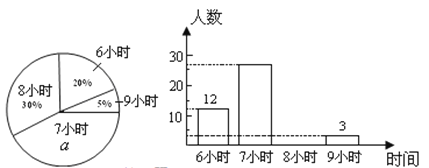
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数
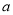 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BM、CN分别是△
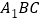 的两个外角的角平分线,
的两个外角的角平分线,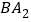 、
、 分别是
分别是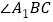 和
和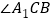 的角平分线,如图①;
的角平分线,如图①;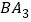 、
、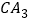 分别是
分别是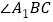 和
和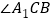 的三等分线(即
的三等分线(即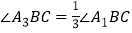 ,
,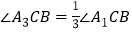 ),如图②;依此画图,
),如图②;依此画图,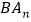 、
、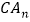 分别是
分别是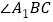 和
和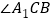 的n等分线(即
的n等分线(即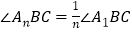 ,
,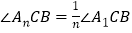 ),
),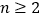 ,且
,且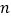 为整数.
为整数.(1)若
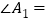
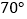 ,求
,求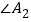 的度数;
的度数;(2)设
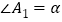 ,请用
,请用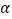 和n的代数式表示
和n的代数式表示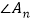 的大小,并写出表示的过程;
的大小,并写出表示的过程;(3)当
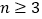 时,请直接写出
时,请直接写出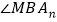 +
+ 与
与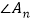 的数量关系.
的数量关系.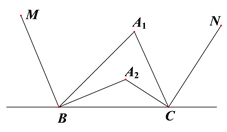
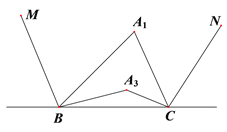
图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】从社会效益和经济效益出发,某地制定了三年规划,投入资金进行生态环境建设,并以此发展旅游产业。根据规划,第一年度投入资金800万元,第二年度比第一年度减少
 ,第三年度比第二年度减少
,第三年度比第二年度减少 。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用:
。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用:  =1.414,
=1.414,  =3.606 计算结果精确到百分位)
=3.606 计算结果精确到百分位)
相关试题

