【题目】如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°. 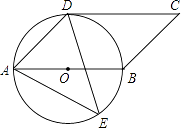
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.
参考答案:
【答案】
(1)解:CD与⊙O相切.
理由:连接OD,
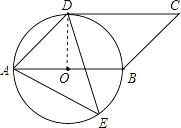
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
即OD⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵AB为直径的圆O经过点D,
∴CD与⊙O相切;
(2)解:过点O作OF⊥AE,连接OE,
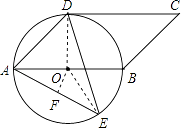
则AF= ![]() AE=
AE= ![]() ×10=5(cm),
×10=5(cm),
∵OA=OE,
∴∠AOF= ![]() ∠AOE,
∠AOE,
∵∠ADE= ![]() ∠AOE,
∠AOE,
∴∠ADE=∠AOF,
在Rt△AOF中,sin∠AOF= ![]() =
= ![]() ,
,
∴sin∠ADE= ![]() .
.
【解析】(1)首先连接OD,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可证得OD⊥AB,又由四边形ABCD是平行四边形,即可证得OD⊥CD,即可证得CD与⊙O相切;(2)首先过点O作OF⊥AE,连接OE,由垂径定理可得AF=5cm,∠AOF= ![]() ∠AOE,又由圆周角定理可得∠ADE=
∠AOE,又由圆周角定理可得∠ADE= ![]() ∠AOE,继而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得答案.
∠AOE,继而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得答案.
【考点精析】本题主要考查了平行四边形的性质和切线的判定定理的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F分别为垂足,则下列四个结论:①∠DEF=∠DFE; ②AE=AF; ③AD平分∠EDF; ④AD垂直平分EF.其中正确结论有()
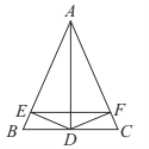
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.求证:
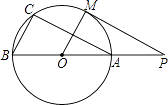
(1)△ABC∽△POM;
(2)2OA2=OPBC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线
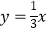 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.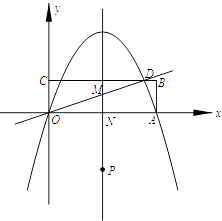
(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )

A.40°
B.50°
C.60°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=
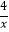 ,下列说法错误的是( )
,下列说法错误的是( )
A.这个函数的图象位于第一、第三象限
B.当x>0时,y随x的增大而增大
C.这个函数的图象既是轴对称图形又是中心对称图形
D.当x<0时,y随x的增大而减小
相关试题

