【题目】如图,线段AB=24cm,O为线段AB上一点,且AO:BO=1:2,C、E顺次为射线AB上的动点,点C从A点出发向点B方向运动,E点随之运动,且始终保持CE=8cm(C点到达B点时停止运动),F为OE中点.
(1)当C点运动到AO中点时,求BF长度;
![]()
(2)在C点运动的过程中,猜想线段CF 和BE是否存在特定的数量关系,并说明理由;
![]()
(3)① 当E点运动到B点之后,是否存在常数n,使得OE-n·CF的值不随时间改变而变化.若存在,请求出n和这个不变化的值;若不存在,请说明理由.
![]()
② 若点C的运动速度为2cm/秒,求点C在线段FB上的时间为 秒(直接写出答案);
参考答案:
【答案】(1)FE=2,BE=12,BF=14cm(2)2CF=BE(3)①16cm ②4秒
【解析】试题分析: (1)先求出 AO,BO的长,再求当C点运动到AO中点时,AC,CE,OE的长. 根据F为OE中点,即可求出BF的长;
(2)设AC=x,分别表示出CO,OE,FE,CF,BE的长 ,即可得到结论;
(3)①设OF=EF=x,得到OE –nCF=(2-n)x+8n ,可以得到当n=2 时,OE -2CF = 16 cm.
② 根据时间=路程÷速度即可得到结论.
试题解析:解:(1)∵AB=24cm,AO:BO=1:2.
∴AO=8,BO=16.当C点运动到AO中点时,AC=4,CE=8,OE=4.
∵F为OE中点,∴FE=2,BE=12,BF=14cm.
(2)设AC=x,CO=8-x,OE=AC=x,FE=FO= FE=FO=![]() x,CF=8-
x,CF=8-![]() x.
x.
BE=24-8-x=16-x ,∴2CF=BE
(3)①设OF=EF=x,OE –nCF=2x-n(x-8)=(2-n)x+8n
当n=2 时, OE -2CF = 16 cm.
② 8÷2=4秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春节黄金周海南旅游大幅增长,据统计,2月7至13日,全省共接待游客约3710000人次,将3710000用科学记数法表示为( )
A.3.71×107
B.0.371×107
C.3.71×106
D.37.1×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(﹣1,
 ),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.
),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.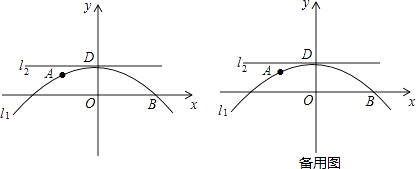
(1)求l1的解析式,并写出它的对称轴和顶点坐标;
(2)设l1上有一动点P从点A出发,沿抛物线从左向右运动,点P的纵坐标yp也随之以每秒2个单位长的速度变化,设点P运动的时间为t(秒),连接OP,以线段OP为直径作⊙F.
①求yp关于t的表达式,并写出t的取值范围;
②当点P在起点A处时,直线l2与⊙F的位置关系是 , 在点P从点A运动到点D的过程中,直线12与⊙F是否始终保持着上述的位置关系?请说明理由;
(3)在(2)条件下,当点P开始从点A出发,沿抛物线从左到右运动时,直线l2同时向下平移,垂足D的纵坐标yD以每秒3个单位长度速度变化,当直线l2与⊙F相交时,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形 B.三个角是直角的四边形是矩形
C.四边相等的四边形是菱形D.有一个角是直角的菱形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3(x﹣2)2+5的顶点在( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )

A. (A) B. (B) C. (C) D. (D)
-
科目: 来源: 题型:
查看答案和解析>>【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
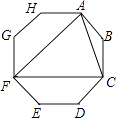
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
相关试题

