【题目】如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①四边形CEDF有可能成为正方形;
②△DFE是等腰直角三角形;
③四边形CEDF的面积是定值;
④点C到线段EF的最大距离为![]() .
.
其中正确的结论是( )
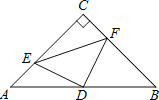
A.①④ B.②③ C.①②④ D.①②③④
参考答案:
【答案】D.
【解析】
试题分析:①当E、F分别为AC、BC中点时,四边形CDFE是正方形,故此选项正确;
②①连接CD;
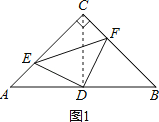
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
∵在△ADE和△CDF中,
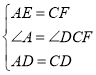
∴△ADE≌△CDF(SAS);
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形.故此选项正确;
③∵△ADE≌△CDF,
∴S△ADE=S△CDF.
∵S四边形CEDF=S△CED+S△CFD,
∴S四边形CEDF=S△CED+S△AED,
∴S四边形CEDF=S△ADC.
∵S△ADC=![]() S△ABC=4.
S△ABC=4.
∴四边形CEDF的面积是定值4,故本选项正确;
④④△DEF是等腰直角三角形,![]() DE=EF,
DE=EF,
当EF∥AB时,∵AE=CF,
∴E,F分别是AC,BC的中点,故EF是△ABC的中位线,
∴EF取最小值=![]() =2
=2![]() ,
,
∵CE=CF=2,
∴此时点C到线段EF的最大距离为![]() EF=
EF=![]() .故此选项正确.
.故此选项正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥形和烟囱帽的底面直径是40cm,母线长是120cm,需要加工这样的一个烟囱帽,请你画一画:
(1)至少需要多少厘米铁皮(不计接头)
(2)如果用一张圆形铁皮作为材料来制作这个烟囱帽,那么这个圆形铁皮的半径至少应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与AC相切于点A,且AB=AC,BC与⊙O相交于点D,下列说法不正确的是().
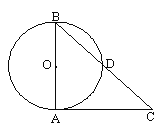
A. ∠C = 45° B. CD=BD C. ∠BAD=∠DAC D. CD=AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正五边形ABCDE的对角线AC、BE相交于M.
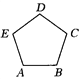
(1)求证:四边形CDEM是菱形;
(2)设MF2=BE·BM,若AB=4,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E,∠4=∠5,请判断AD与BC的位置关系,并证明你的结论.
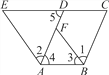
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
相关试题

