【题目】如图所示,正五边形ABCDE的对角线AC、BE相交于M.
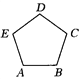
(1)求证:四边形CDEM是菱形;
(2)设MF2=BE·BM,若AB=4,求BE的长.
参考答案:
【答案】(1)证明见解析(2)2+2![]()
【解析】试题分析:(1)先证明CDEM是平行四边形,由于DE=DC,所以是菱形.
(2) 先证明△ABE∽△MAB,得到AB2=BEBM;ME2=BEBM,可解得BE长..
试题解析:
(1)∵五边形ABCDE是正五边形,
∴∠D=![]() ×
×![]() ×360°=108°,∠DCA=
×360°=108°,∠DCA=![]() ×
×![]() ×360°=72°,
×360°=72°,
∴∠D+∠DCA=180°,
∴DE∥AC;同理可证DC∥BE,
∴四边形DEMC为平行四边形,而DE=DC,
∴四边形CDEM是菱形.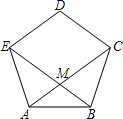
(2)∵五边形ABCDE是正五边形,
∴∠AEB=![]() ×
×![]() ×360°=36°,∠EAM=
×360°=36°,∠EAM=![]() ×
×![]() ×360°=72°;
×360°=72°;
同理可求∠BAC=∠ABE=36°,
∴△ABE∽△MAB,
∴AB:BE=BM:AB,
∴AB2=BEBM;
∵ME2=BEBM,
∴ME=AB=4,BM=BE-4,
∴BE(BE-4)=16,
解得:BE=2+2![]() 或2-2
或2-2![]() (舍去).
(舍去).
-
科目: 来源: 题型:
查看答案和解析>>【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与AC相切于点A,且AB=AC,BC与⊙O相交于点D,下列说法不正确的是().
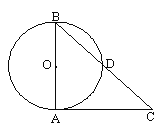
A. ∠C = 45° B. CD=BD C. ∠BAD=∠DAC D. CD=AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①四边形CEDF有可能成为正方形;
②△DFE是等腰直角三角形;
③四边形CEDF的面积是定值;
④点C到线段EF的最大距离为
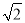 .
.其中正确的结论是( )
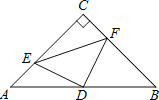
A.①④ B.②③ C.①②④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E,∠4=∠5,请判断AD与BC的位置关系,并证明你的结论.
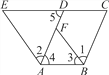
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯
电量
电价
一档
0~180度
0.6元/度
二档
181~400度
二档电价
三档
401度及以上
三档电价
相关试题

