【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.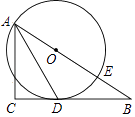
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】
(1)
证明:连接OD,
∵BC是⊙O的切线,
∴OD⊥BC,又∠C=90°,
∴OD∥AC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,即AD平分∠BAC
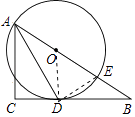
(2)
解:连接CE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠CAD,tan∠DAC= ![]() ,
,
∴tan∠EAD= ![]() ,
,
∵tan∠DAC= ![]() ,AC=8,
,AC=8,
∴CD=6,
由勾股定理得,AD= ![]() =10,
=10,
∴ ![]() =
= ![]() ,
,
解得,DE= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴⊙O的半径为 ![]() .
.
【解析】(1)连接OD,根据切线的性质得到OD⊥BC,根据平行线的性质和等腰三角形的性质证明;(2)连接CE,根据正切的定义和勾股定理求出AD,根据正切的定义计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的材料,然后解答问题.
通过计算,发现:
方程x+
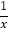 =2+
=2+ 的解为x=2或x=
的解为x=2或x= ;
;方程x+
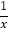 =3+
=3+ 的解为x=3或x=
的解为x=3或x= ;
;方程x+
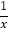 =4+
=4+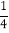 的解为x=4或x=
的解为x=4或x=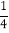 ;
;…
(1)观察猜想:求关于x的方程x+
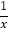 =n+
=n+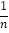 的解;
的解;(2)实践运用:对于关于x的方程x-
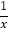 =m-
=m- 的解,小明观察得“x=m”是该方程的一个解,请你猜想该方程的另一个解,并用方程的解的概念对该解进行验证;
的解,小明观察得“x=m”是该方程的一个解,请你猜想该方程的另一个解,并用方程的解的概念对该解进行验证;(3)拓展延伸:请利用上面的规律,求关于x的方程x+
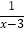 =a+
=a+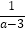 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC=
 .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= 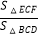 .
.
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190﹣2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
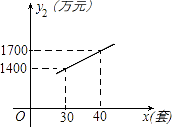
(1)直接写出y2(2)与x之间的函数关系式;
(2)求月产量x的取值范围;
(3)当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数
 的图像经过点A(-1,1),下列各点中在该函数图象上的是( )
的图像经过点A(-1,1),下列各点中在该函数图象上的是( )A. (1,5) B. (2,5) C. (-2,-2) D. (0,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点
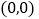 ,3的对应点是
,3的对应点是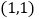 ,16的对应点是
,16的对应点是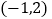 .那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.
.那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.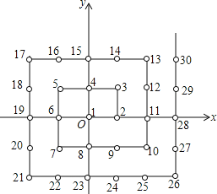
相关试题

