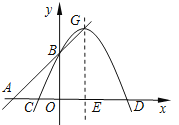
【题目】已知二次函数y=ax2-4ax+a2+2(a<0)图像的顶点G在直线AB上,其中A(![]() ,0)、B(0,3),
,0)、B(0,3),
对称轴与x轴交于点E.
(1)求二次函数y=ax2-4ax+a2+2的关系式;
(2)点P在对称轴右侧的抛物线上,且AP平分四边形GAEP的面积,求点P坐标;
(3)在x轴上方,是否存在整数m,使得当![]() < x ≤
< x ≤![]() 时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
参考答案:
【答案】(1)二次函数关系式为y=-x2+4x+3;
(2)P(![]() ,
, ![]() ),
),
(3)m取-2、-1
【解析】解(1)由A(-![]() ,0)、B(0,3),可设直线AB:y=kx+3,
,0)、B(0,3),可设直线AB:y=kx+3,
从而得,k=2, ∴y=2x+3,
抛物线y=ax2-4ax+a2+2的顶点G(2,a2-4a+2),
点G在直线AB上,∴ a2-4a+2=4+3,∴a=-1,a=5(舍去),
二次函数关系式为y=-x2+4x+3.
(2)∵AP平分四边形GAEP的面积, ∴2S△AEP=S四边形GAEP,
设P(t,-t2+4t+3),
∴ 2×![]() (2+
(2+![]() )(-t2+4t+3)=
)(-t2+4t+3)=![]() ×7×(2+
×7×(2+![]() )+
)+![]() ×7×(t-2)
×7×(t-2)
∴ 2t2-6 t-3=0,∴t1=![]() , t2=
, t2=![]() (舍去)∴P(
(舍去)∴P(![]() ,
, ![]() ),
),
(3)抛物线与x轴交点C(2-![]() ,0),D(2+
,0),D(2+![]() ,0),
,0),
在x轴上方,抛物线y随x增大而减大,则2-![]() <x≤2,
<x≤2,
又∵![]() < x≤
< x≤![]() ,
,
∴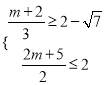 ,得:4-3
,得:4-3![]() ≤m≤-
≤m≤-![]() ,
,
∵整数m为整数,∴m为-3,-2、-1.
又∵![]() <
<![]() ,m>-
,m>-![]() .
.
∴m取-2、-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数图象经过(﹣1,0),(3,0),(1,﹣8)三点,求此函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=
 x-2与直线y=-
x-2与直线y=- x+a相交于x轴上,则直线y=-
x+a相交于x轴上,则直线y=- x+a不经过( )
x+a不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,一次函数y=
 x+3
x+3 的图象与x轴、y轴分别交于A、B,平行四边形ABCD中,D(6,0),函数y=
的图象与x轴、y轴分别交于A、B,平行四边形ABCD中,D(6,0),函数y=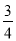 x+m图象过点E(4,0),与y轴交于G,动点P从O点沿y轴正方向以每秒2个单位的速度出发,同时,以P为圆心的圆,半径从6个单位起以每秒1个单位的速度缩小,设运动时间为t.
x+m图象过点E(4,0),与y轴交于G,动点P从O点沿y轴正方向以每秒2个单位的速度出发,同时,以P为圆心的圆,半径从6个单位起以每秒1个单位的速度缩小,设运动时间为t.(1)若⊙P与直线EG相切,求⊙P的面积;
(2)以CD为边作等边三角形CDQ,若⊙P内存在Q点,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B两个村庄的坐标分别为(2,3),(6,4),一辆汽车从原点O出发在x轴上行驶.
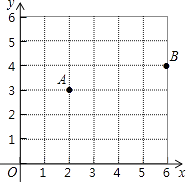
(1)汽车行驶到什么位置时离A村最近?写出此点的坐标;
(2)汽车行驶到什么位置时离B村最近?写出此点的坐标;
(3)汽车行驶到什么位置时,距离两村的和最短?请在图中画出这个位置,并求出此时汽车到两村距离的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
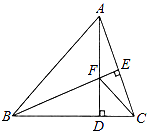
(1)求证:BF=2AE;
(2)若CD=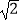 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象如图,则k、b的符号是( )
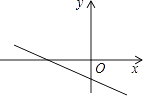
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
相关试题

